皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
試験前の白熱期のせいか、当ブログのPV数が急上昇しています!ありがとうございます!
訪問者の傾向を見てみますと、「電験一種」で来る方が大多数を占めています。ということで、電験1種系の記事を書けばPVはもっと上がるということが分かるのですが、如何せん3種の記事を書きたくて1種に回す時間がありません笑
ブログ運営においてこのようなことが非合理的であるのは重々承知の上で3種の記事を書いていきます笑
今回はパワエレのチョッパ記事の完結編ということで、パワエレの過去問
の解説をしていきます。
平成19年の方は、正直解いてみてとても難しいと感じました。電験2種二次試験でパワエレを捨ていてただけはあります汗 やはり、私自身パワエレにはまだブラックボックスなところがありますね。
ということで、色んなところの解説と検索を駆使して、それぞれ書いていきます!
平成19年 問16(b)

(4)が正解となる理由
\(\alpha =0\)の条件の下、\(\phi =0,\frac{\pi}{2}\)という極端な例を考えてみます。
\(\phi=0\)のときは負荷が純抵抗負荷であることと同じなので、
- ターンオフするときは電流=0となるとき
- 純抵抗のとき電流と電圧は同位相となるため、電流=0と電圧=0は同じタイミング
つまり、ターンオフ時には抵抗に電圧はかからず、電源にも起電力が発生しないので、その間にあるサイリスタにも電圧は印加されません。
\(\phi=\frac{\pi}{2}\)のときは、負荷がコイルのみであることと同じなので、
- ターンオフするときは電流=0となるとき
- 純粋なコイルのとき電流は電圧より位相が\(\frac{\pi}{2}\)遅くなるため、電流=0のとき電圧はマイナス側に最大となる
つまり、ターンオフ時には抵抗に絶対値での最大電圧がかかります。このタイミングでターンオフすると、電流の流れていない抵抗部分は導線とみなせるので、サイリスタ部分にダイレクトに最大電圧がかかったということになります。
ということで、(4)は誤りです。
平成22年 問16(b)
公式の導出
コチラの「整流回路について(単相)」で紹介したものと同じ導出を行います。
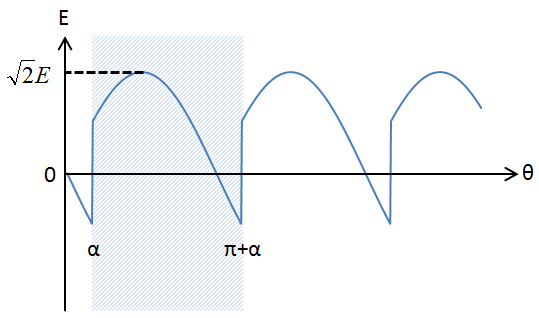
繰り返しの区間の1つ\(\alpha \leqq \theta \leqq \alpha +\pi\)について、
\begin{align}
E_{\mathrm{d}}&=\frac{\displaystyle \int_\alpha^{\alpha +\pi} \sqrt{ 2 }E\sin\theta \mathrm{d}\theta}{\pi}\\
&=\frac{\left[ -\sqrt{ 2 }E\cos\theta \right]_\alpha^{\alpha +\pi}}{\pi}\\
&=\frac{-\sqrt{ 2 }E[\cos(\alpha +\pi) -\cos\alpha]}{\pi}\\
\end{align}
ここに、加法定理より
\begin{align}
\cos(\alpha +\pi)&=\cos\alpha \cos\pi -\sin\alpha \sin\pi\\
&=\cos\alpha \times (-1) -\sin\alpha \times 0\\
&=-\cos\alpha\\
\end{align}
を代入して
\begin{align}
E_{\mathrm{d}}&=\frac{-\sqrt{ 2 }E(-\cos\alpha -\cos\alpha)}{\pi}\\
&=\frac{2\sqrt{ 2 }E\cos\alpha}{\pi}\\
\end{align}
となります。
これに\(\alpha =\frac{\pi}{2}\)を代入して\(E_\mathrm{d}=0\)となります。
条件「負荷のインダクタンス\(L[\mathrm{H}]\)が大きく、制御角\(\alpha\)が小さいとき」について
「負荷のインダクタンス\(L[\mathrm{H}]\)が大きい」とは、コイルの特性が大きい、つまり一定電流を流す性質が強いという意味です。きれいな直流電流を生成する際は、電流値の脈動をできるだけ抑える必要があるため、コイルの特性を際だたせるようにすることはよくやる手法かと思います。
また、「制御角が小さい」と言うのを具体的に言うと、先程の公式の直流電圧が0以上となる範囲のことを言います。つまり、\(\alpha \leqq \pi\)です。これを越えると、電圧が負になってしまい、正の直流電圧を作ることができなくなります。
まとめ
ブラックボックスがあるのを自覚しながら記事を書いていったので、不完全燃焼感がありありです。奥歯にものが詰まった感じがありましたら申し訳ないです。
パワエレに関する記事はこれにて終了としまして、次回は微分方程式に関する記事を2つほど書こうかと思います。こちらは得意な数学のウェイトが高いので、今回よりかは自身があります笑
ちなみに、パワエレの種類解説から始まったこれら


の記事は読者の方からコメントを頂いて書いたものです。
気になる・分からない単元がおありの場合は、問い合わせフォームなりコメントなりでいただければ遅筆ですができるだけ記事作成で対応していきます。
当ブログへのネタ提供をよろしくお願い致します。
それでは次回!













ケンタさんおはようございます!
今回の記事も数式あり、図解ありで、大変だったかと思います。
ありがとうございました。
私の希望では、合格体験記を読むのが好きなのと、来年の夏に向けて準備したいのとで、2種一次試験の攻略方法など教えていただけると嬉しいです。
>やまさきさん
いつもコメントありがとうございます!
そうですね。
今は微分方程式についての記事を書いていますので、そのシリーズが終わったら合格体験記の歯抜けを補完していきます。
過去問再挑戦が終わるのを待っているといつになるかわからないので笑
ケンタさん、いつもありがとうございます。
私は三種の時ですら、公式を丸々暗記するのではなく、回路の見方と公式の導き方と
やらないと問題が解けないタイプだったので、今回の記事は大変参考になりました。
(と、いうかあの膨大な公式数を覚えて試験に臨む人はマジ尊敬します)
公式の導式のやり方ですと、もし公式を忘れたとしても「力業」で解けすもんね。
やはり、パワエレは楽しいです。これが三相不平衡(且つ、事故発生)とかだったら
一気に凹んだかも知れないです。とはいうもののあれも落ち着いて回路図とベクトル
図を丁寧に書けば実際は解ける、ということになっている、はず。
そしていよいよ電験試験本番ですね。
三種で終わったー、と思っている(た)、私は今のところは高みの見物ですけど
時勢を省みたり、勉強そのものに興味をもっている状態ですので
二種にチャレンジしてみようか、という気持ちに段々になってきています。
ですけど、ネックは試験のためには前泊しないといけないんですね・・・。
ということは金曜日から休まないといけないところですね・・・・・。
田舎者の辛いところです。
これからも記事を期待しています。
(やっぱ、ケンタさんは先生向きだと思うんですけど・・・せめて出版を・・・)
>田舎ビルメンさん
いつもコメントありがとうございます!
2種の勉強量は、3種を1から学び直す以上の量になるのは必至です。。
それでも取ろうとされてるのであれば、素晴らしい、の一言です。
公式を公式のまま覚えようとされなかったとこから、田舎ビルメンさんは計算問題の下地ができているかもしれませんね。
何はともあれ頑張って下さい!
今回の記事で思い知りましたが、やはり講師をするなら、何に対しても切り返せるバックグラウンドが必要だと思います。
それを考えると、得意なところだけを記事に書いていた方が気楽かもしれません。