感覚で解く過渡現象

皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。

試験を受験された方はお疲れ様でした。

さて、本日のテーマは「過渡現象」です。試験後に書く内容ではないかもしれませんがお付き合いください笑

パワエレ編に引き続き、これまた数回に渡るであろうテーマの初回は「感覚で解く過渡現象」です。

過渡現象って、真面目にやると微分方程式を解く必要があって、方程式を解こうにも変数分離法や特性方程式など、何パターンかの解法を全て覚えておかないといけないんですよね。

それとは別に幾つかの積分公式も覚えないといけませんし、正攻法で解くと試験時間が足りなくなることがよくあるのではないでしょうか。

実は、過渡現象って簡単な回路図であれば、何となくで\(\frac{\mathrm{d}}{\mathrm{d}t}\)の立式を経ずにいきなり答えを出すことができます。

ケンタ

完全に私オリジナルの方法ですので、数学的正確さに関するツッコミは無しでお願いします笑　100%経験則のやり方です。

【2018.12.19更新】当記事は新電気2018年12月号にも掲載されています。

今回のゴール

今回お伝えする方法をマスターすると、

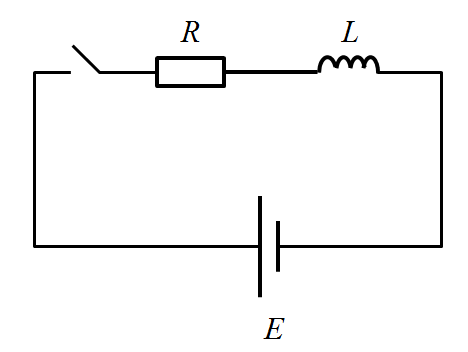
という図を見たら、

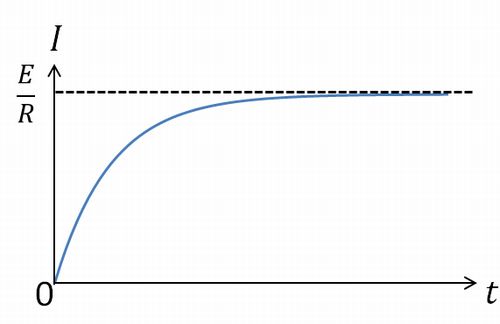
というグラフを自分でかいた後に、余白に少し数文字書くと

\begin{align}
I&=\frac{E}{R}(1-\mathrm{e}^{-\frac{R}{L} t})\\
\end{align}

をいきなり書き出す事ができるようになります。本当です笑

ということで、騙されたと思って読み進めてみて下さい。

\(RL\)直列回路

上図について電流の過渡式を作る方法について説明していきます。

STEP1.グラフをかく

先ず、グラフの概形を決めます。

スイッチを入れた直後の\(t=0\)では、コイルは電流を流そうとしないので\(I=0\)となります。十分時間が経った後は、コイルが流れを妨げるほどの電流変化が無くなりコイルは導線とみなせるようになるので、\(I=\frac{R}{E}\)に漸近していきます。

つまり、以下の図のような挙動となります。

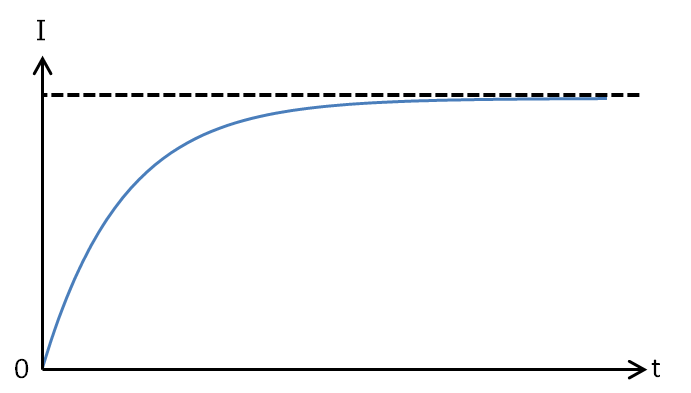
STEP2.時定数部分を求める

こんな単純な回路の時定数を求める、と書いていることから分かるように、私は\(RL\)直列回路の時定数も\(RC\)直列回路の時定数も暗記していません。毎回導出というかなんというか、作り出しています。

今回は直流電源ですが、交流のインピーダンス\(R[\mathrm{\Omega}]\)と\(\omega L[\mathrm{\Omega}]\)を持ってきます。これら２つの比を作ると、\(\frac{R}{\omega L}\)は無次元となります。

この無次元の比に、これまた無次元の\(\omega t\)を掛けると、次元的にはもちろん無次元となます。もう少し変形すると

\begin{align}
\frac{R}{\omega L}\times \omega t&=\frac{R}{L}t\\
&=\frac{ t }{\frac{L}{R}}\\
\end{align}

つまり、\(\frac{L}{R}\)が時定数\(\tau\)となります。

STEP3.グラフから立式する

STEP1でかいたグラフを表す式を立てていきます。

立式の起点は

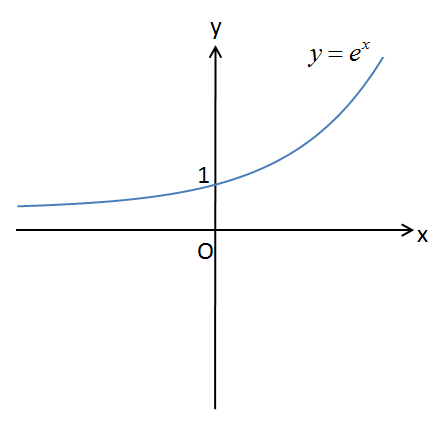
の形です。

過渡現象における指数関数の底は必ず\(\mathrm{e}\)となります。数学的な理由としては、微分方程式の途中で

\begin{align}
\displaystyle \int \frac{\mathrm{d}x}{x}&=\log_\mathrm{e} x+C\\
\end{align}

の公式を使うからです。

感覚的な理由としては、指数関数的な挙動をする自然現象は自然対数の底\(\mathrm{e}\)で表されることが多いからです。

ということで、\(y=\mathrm{e}^x\)からスタートしまして、以下のように変形していきます。

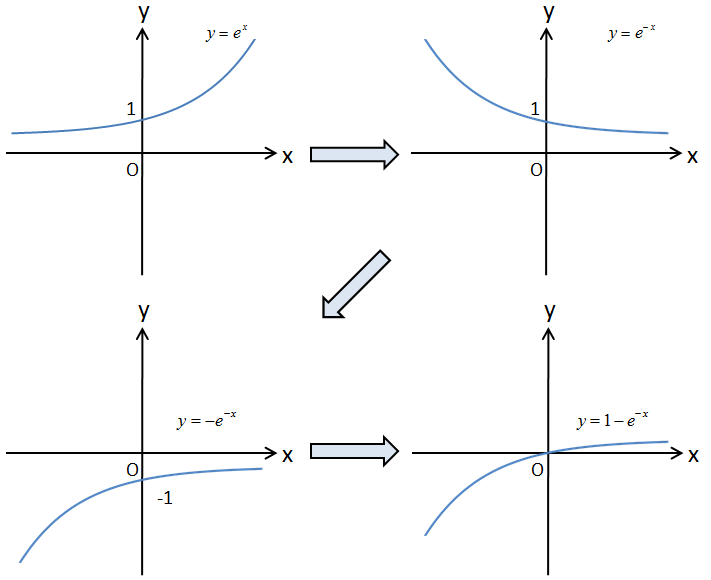
ここまで来たら、\(y\)を\(I\)に、\(x\)を\(\frac{t}{\tau}=\frac{R}{L} t\)に置き換えます。

つまり、

\begin{align}
I&=1-\mathrm{e}^{-\frac{R}{L} t}\\
\end{align}

となります。

STEP4.\(t \to \infty\)を求める

\begin{align}
I&=1-\mathrm{e}^{-\frac{R}{L} t}\\
\end{align}

ではグラフの形は合っていますが、\(t\to \infty\)のときをうまく表せてはいません。

ケンタ

このままでは、\(t\to \infty\)のとき\(I=1\)となってしまいます。

STEP1の図では\(t\to \infty\)のとき、\(I\)は\(\frac{E}{R}\)に漸近していきます。

つまり、頭に\(\frac{E}{R}\)を付けて、

\begin{align}
I&=\frac{E}{R}(1-\mathrm{e}^{-\frac{R}{L} t})\\
\end{align}

を作ります。

なお、

\begin{align}
I&=\frac{E}{R}-\mathrm{e}^{-\frac{R}{L} t}\\
\end{align}

としてしまうと、\(t=0\)のときに\(I=0\)となりません。

おまけ：\(RC\)直列回路

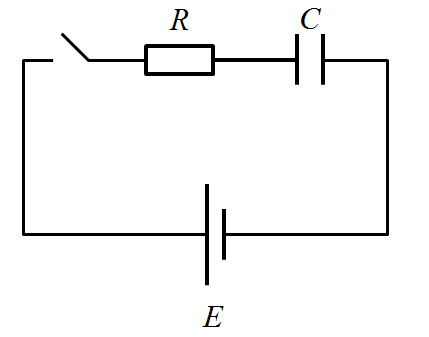
\(RC\)直列回路でも同様にして電流の過渡式を求めることができます。

STEP1.グラフをかく

説明を省きますが、以下のような形となります。

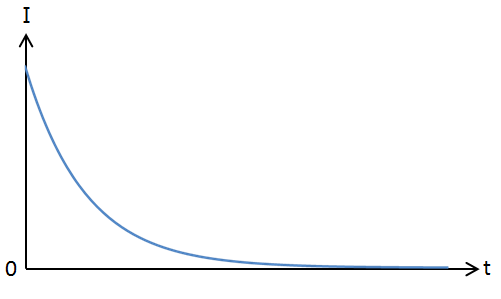
STEP2.時定数部分を求める

\(R\)と\(\frac{1}{\omega C}\)の比を作ると、

\begin{align}
\frac{\frac{1}{\omega C}}{R}&=\frac{1}{R\omega C}\\
\end{align}なります。

この比に、\(\omega t\)を掛けると、

\begin{align}
\frac{1}{R\omega C}\times \omega t&=\frac{t}{RC}\\
\end{align}

つまり、\(RC\)が時定数\(\tau\)となります。

STEP3.グラフから立式する

グラフの形から

\begin{align}
y&=\mathrm{e}^{-x}\\
\end{align}

を作れるので、

\begin{align}
I&=\mathrm{e}^{-\frac{t}{RC}}\\
\end{align}

となります。

STEP4.\(t=0\)を求める

\(t=0\)のとき\(C\)を導線とみなして、

\begin{align}
I&=\frac{E}{R}\\
\end{align}

となります。つまり、頭に\(\frac{E}{R}\)を付けて、

\begin{align}
I&=\frac{E}{R} \mathrm{e}^{-\frac{t}{RC}}\\
\end{align}

となります。

注意！！

今回説明した方法は単純な回路にしか通用しません。

\(RLC\)直列回路

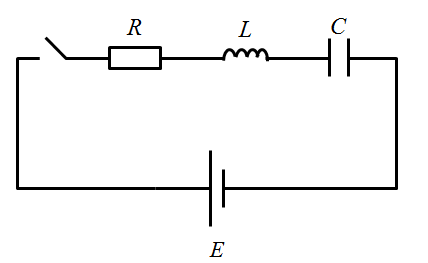
なり、\(RLC\)直並列回路

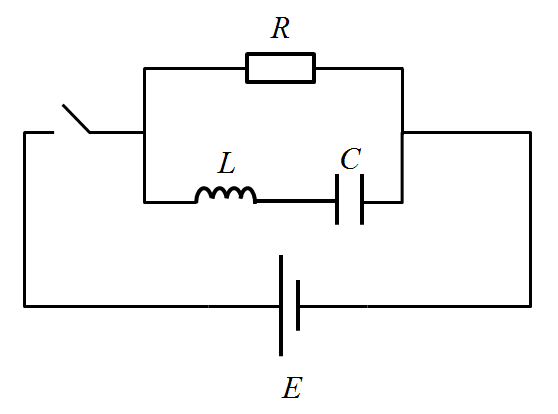
では、電流の過渡式はおろかグラフの概形図もかけません。

これらの回路の電流挙動を調べる場合は、微分方程式なりラプラス変換なりを使用する必要があります。

なぜ、ここで機械・制御に出てくる「ラプラス変換」が登場してきたかは次回のお楽しみということで…

まとめ

今回の方法は

などに使うと便利な方法です。

過渡現象にはこれ以外にも、ショートカットできる方法がもう1つあります。

（私が知っているのがもう１つというだけで、他に沢山方法があるかもしれません。）

それでは次回！

ラプラス変換で解く過渡現象皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。 Twitterや2chでは合格・不合格の阿鼻叫喚となってい...