オペアンプをまとめて覚える方法

皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。

オペアンプってありますよね。

電験３種、２種ともによく出題される単元ですが、２種レベルになってくると回路の種類が増えてきて、2種類→5種類と2.5倍となります。

と言っても、2.5倍となっても公式の導出はワンパターンですので、それを覚えてしまえば回路図を見てからの判断ができますし、特殊な回路図のオペアンプの問題でも、基本的にはこの記事の導出ができるようになれば自然と解けるようになります。

どこかで聞いた話ですね笑　そうです、チョッパー回路でも似たような話をしました。

パワーエレクトロニクスの対策～チョッパ編～皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。 遂に試験まであと１週間ですね。 土曜に電験１・２種一次試...

ということで今回はオペアンプの公式導出の話です。

ケンタ

この話しぶりから分かるように、私は毎回公式を導出して対処しています。特に積分器と微分器についてはコンデンサの位置で名称と積分 or 微分が変わるので、導出を覚えるしかありません。

オペアンプとは？

opeampという英単語があるわけではなく、造語です。

省略せずに書くとOPErational AMPlifierとなり、日本語では演算増幅器と訳されます。

このoperational（演算）と言うところに、オペアンプの基本的な動作が集約されているような気がします。

基本的な動作

オペアンプの典型的な回路図に基づいて説明してきます。

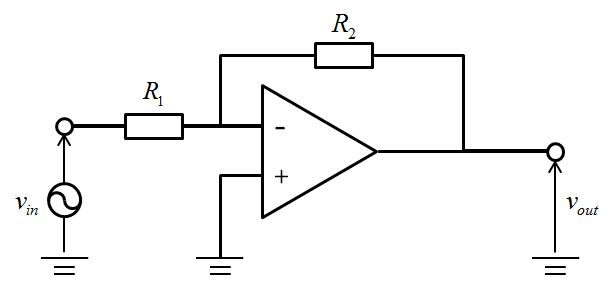
オペアンプの基本的な動作は、＋と－の入力電位の差が無くなるように\(v_{\mathrm{out}}\)の電位を調整することです。

＋と－間には大きさ無限大の入力インピーダンスがあるので、＋と－の入力電位の差が無くなっても↓のような電流の流れが発生せず、

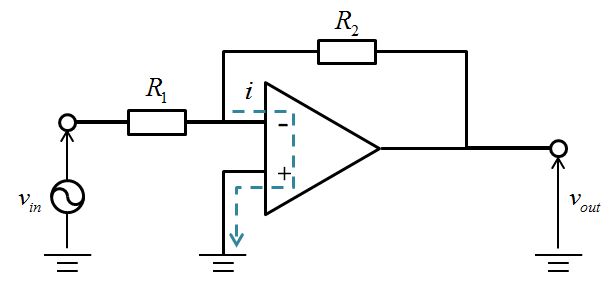
分岐しない一筆書きの電流の流れとなります。

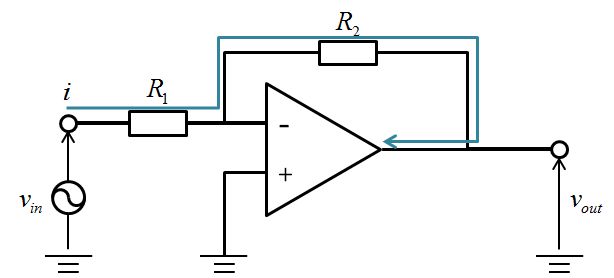
反転増幅器

前出の図について説明を続けます。

\(R_1\)の右端はイマジナリショートを介して大地に電流が流れずとも接地をしているので、その電位は0とみなすことができます。よって、\(R_1\)を流れる電流\(i\)は

\begin{align}
v_{\mathrm{in}}&=R_1i\\
i&=\frac{v_{\mathrm{in}}}{R_1}\\
\end{align}

となります。これを使って\(i\)の経路にわたって電圧降下の式を立てると、

\begin{align}
v_{\mathrm{in}}&=(R_1+R_2)i+v_{\mathrm{out}}\\
v_{\mathrm{in}}&=(R_1+R_2)\times \frac{v_{\mathrm{in}}}{R_1}+v_{\mathrm{out}}\\
v_{\mathrm{in}}&=v_{\mathrm{in}}+\frac{R_2}{R_1}v_{\mathrm{in}}+v_{\mathrm{out}}\\
\frac{v_{\mathrm{out}}}{v_{\mathrm{in}}}&=-\frac{R_2}{R_1}\\
\end{align}

となります。

出力比\(v_{\mathrm{out}}/v_{\mathrm{in}}\)がマイナスとなるので、この増幅器は反転増幅器となります。\(v_{\mathrm{in}}\)に対して、\(v_{\mathrm{out}}\)は反対の電位となって出力されます。

導出のポイントは主に2つです。

以降も、与えられた回路図に対して↑のポイントにしたがって導出をしていきます。

それではどんどん行きましょう！

非反転増幅器

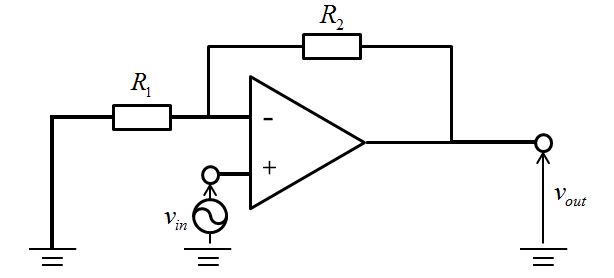
この回路図では＋の入力電位が\(v_{\mathrm{in}}\)となるので、－の入力電位がイマジナリショートのためにつられて\(v_{\mathrm{in}}\)となります。

そのため、電流の向きが↓のようになり、オペアンプの先から電流が供給されます。

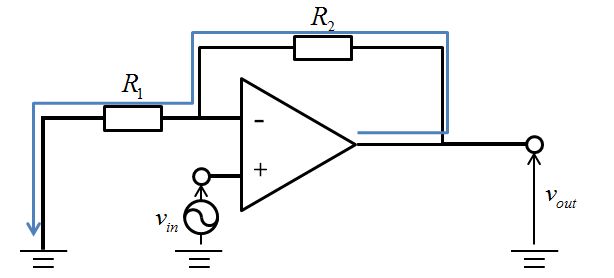
その値\(i\)は

\begin{align}
v_{\mathrm{in}}&=R_1i\\
i&=\frac{v_{\mathrm{in}}}{R_1}\\
\end{align}

となります。これを使って\(i\)の経路にわたって電圧降下の式を立てると、

\begin{align}
v_{\mathrm{in}}+R_2i&=v_{\mathrm{out}}\\
v_{\mathrm{in}}+R_2\times\frac{v_{\mathrm{in}}}{R_1}&=v_{\mathrm{out}}\\
\frac{R_1+R_2}{R_1}v_{\mathrm{in}}&=v_{\mathrm{out}}\\
\frac{v_{\mathrm{out}}}{v_{\mathrm{in}}}&=\frac{R_1+R_2}{R_1}\\
\end{align}

となります。

出力比\(v_{\mathrm{out}}/v_{\mathrm{in}}\)がプラスとなるので、この増幅器は非反転増幅器となります。つまり、\(v_{\mathrm{in}}\)と\(v_{\mathrm{out}}\)は常に同じ符号の電位となって出力されます。

差動増幅器

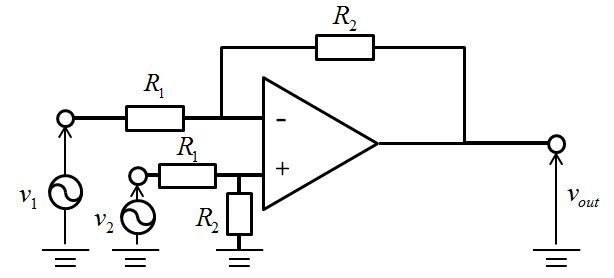
この回路図では＋の入力電位が\(v_2\)を按分した値\(\frac{R_2}{R_1+R_2}v_2\)となるので、－の入力電位がイマジナリショートのためにつられて同じ値となります。

そのため、\(R_1\)を流れる電流\(i\)は

\begin{align}
v_{1}-\frac{R_2}{R_1+R_2}v_2&=R_1i\\
i&=\frac{v_{1}}{R_1}-\frac{R_2}{R_1(R_1+R_2)}v_2\\
\end{align}

となります。これを使って\(i\)の経路にわたって電圧降下の式を立てると、

\begin{align}
v_1&=(R_1+R_2)i+v_{\mathrm{out}}\\
v_1&=\frac{R_1+R_2}{R_1}v_1-\frac{R_2}{R_1}v_2+v_{\mathrm{out}}\\
-\frac{R_2}{R_1}v_1+\frac{R_2}{R_1}v_2&=v_{\mathrm{out}}\\
v_{\mathrm{out}}&=-\frac{R_2}{R_1}(v_1-v_2)\\
\end{align}

となります。2つの電圧源を使って入力電位を作るので、差動増幅器と呼ばれます。

積分器

ここからはコンデンサが登場してきて、少し難易度が上がってきます。

交流電源回路におけるコンデンサを含む電圧降下の式では、\(\mathrm{j}\omega\)が使用されますが、増幅器に限っては直流回路的に微積分を使って表します。コンデンサを使った微積分の表現は、中々慣れていない方が多いと思いますので、丁寧に解説していきます。

先ず、反転増幅器と同じように電流\(i\)を導出します。

\begin{align}
i&=\frac{v_{\mathrm{in}}}{R_1}\\
\end{align}

です。次に電圧降下の式を立てます。

コンデンサの電圧を\(v_\mathrm{C}\)とすると、

\begin{align}
v_{\mathrm{in}}&=R_1i+v_\mathrm{C}+v_{\mathrm{out}}\\
\end{align}

となります。

ここで、\(v_\mathrm{C}\)を\(i\)を使った式に変換していきます。

コンデンサ関係の公式で\(v\)が登場してくるものと言えば、

\begin{align}
Q&=CV\\
\end{align}

ですので、

\begin{align}
v_\mathrm{C}&=\frac{Q}{C}\\
\end{align}

となります。次に、電荷\(Q\)と電流\(i\)の関係式は

\begin{align}
Q&=\displaystyle \int i\mathrm{d}t\\
\end{align}

ですので、

\begin{align}
v_\mathrm{C}&=\frac{1}{C}\displaystyle \int i\mathrm{d}t\\
\end{align}

となります。

以上のことから、電圧降下の式は以下となります。

\begin{align}
v_{\mathrm{in}}&=R_\mathrm{1i}+v_\mathrm{C}+v_{\mathrm{out}}\\
v_{\mathrm{in}}&=R_1\times\frac{v_{\mathrm{in}}}{R_1}+\frac{1}{C}\displaystyle \int \frac{v_{\mathrm{in}}}{R_1}i\mathrm{d}t+v_{\mathrm{out}}\\
v_{\mathrm{out}}&=-\frac{1}{R_1C}\displaystyle \int v_{\mathrm{in}}i\mathrm{d}t\\
\end{align}

上式に積分記号\(\displaystyle \int\)が登場してくるので、この回路は積分器と呼ばれます。

微分器

今度はコンデンサの位置が違う場合です。

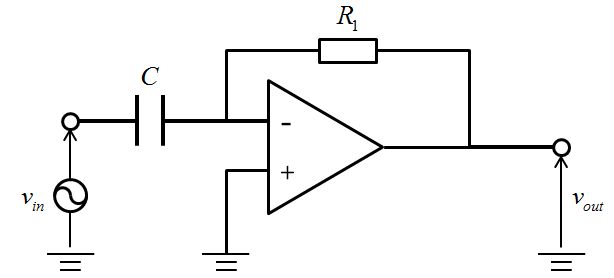
この場合でも先ず、イマジナリショートについて記述します。コンデンサの両端の電位差は\(v_1-0=v_1\)ですので、

\begin{align}
Q&=Cv_{\mathrm{in}}\\
\displaystyle \int i\mathrm{d}t&=Cv_{\mathrm{in}}\\
\end{align}

となります。イマジナリショートの条件からは\(i\)の式を作る、というのがこれまでの流れでしたので、今回も両辺を\(t\)で微分して\(i\)の式を作ります。

\begin{align}
\frac{\mathrm{d}}{\mathrm{d}t}(\displaystyle \int i\mathrm{d}t)&=\frac{\mathrm{d}}{\mathrm{d}t}(Cv_{\mathrm{in}})\\
i&=C\frac{\mathrm{d}v_{\mathrm{in}}}{\mathrm{d}t}\\
\end{align}

となります。

次に、\(i\)の経路にわたって電圧降下の式を立てると、

\begin{align}
v_{\mathrm{in}}&=v_{\mathrm{C}}+R_1i+v_{\mathrm{out}}\\
v_{\mathrm{in}}&=v_{\mathrm{in}}+R_1i+v_{\mathrm{out}}\\
v_{\mathrm{out}}&=-R_1i\\
&=-R_1 C\frac{\mathrm{d}v_{\mathrm{in}}}{\mathrm{d}t}\\
\end{align}

となります。上式に微分が登場してくるので、この回路は微分器と呼ばれます。

 まとめ

 いかがでしたでしょうか。

種類の多いオペアンプでも、以下の2つのことを意識すれば網羅的に導出できることを実感できたのではないでしょうか。（重要なポイントですので、もう１度載せておきます。）