皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
電験の電磁気学の分野は覚えなくてはいけない公式がたくさんあります。それに加えて地味に面倒なのが、公式で計算された量のベクトルの向きまでも覚える必要があることです。
このベクトルの向きは「フレミングの左手の法則」とかで対処することができるはするのですが、「フレミングの右手の法則」があったりと、結構混乱するのではないでしょうか。
私は、このベクトルの向きは「右ねじの法則」で全て対応するようにしています。参考書では、「右ねじの法則」は電流とその同心状の磁界の向きにしか使うときがないですが、この法則は拡張性が高くて、実はかなり便利です!
それでは説明していきます!
ベクトルの外積

いきなり専門用語を出してすみません。電磁気学の公式を説明していく上で、必要な考え方ですので、少し寄り道して説明していきます。
ベクトルの内積
電験ではベクトルという概念が登場はするものの、ベクトルの内積を取り扱うことはないです。ということで、説明を省略しても良いのですが、今回説明したい外積と似たような用語ですので、一応説明しておきます。
\(\vec{ a }=\left( \begin{array}{c} a_1 \\ a_2 \end{array} \right)\)と\(\vec{ b }=\left( \begin{array}{c} b_1 \\ b_2 \end{array} \right)\)が与えられているとき
\begin{align}\vec{ a } \cdot \vec{ b }&=\left( \begin{array}{c} a_1 \\ a_2 \end{array} \right) \cdot \left( \begin{array}{c} b_1 \\ b_2 \end{array} \right)\\
&=a_1 b_1+a_2b_2\\ \end{align}
を内積と言います。内積は
\begin{align}\vec{ a } \cdot \vec{ b }&=|\vec{ a }||\vec{ b }|\cos\theta\\ \end{align}
という表記もできることから、\(\vec{ a }\)を力、\(\vec{ b }\)を距離とすれば、\(\vec{ a } cdot \vec{ b }\)は力がした仕事を表します。
この公式の導出は省略しますが、ベクトルの内積で注意してほしいのは、ベクトル同士を内積するとスカラー量になるということです。というかそもそも出題されませんので、注意しておく必要もないかもしれません笑
一方で、ベクトル量は方向も大きさもある量のことです。[/chat]
ベクトルの外積
ベクトルの外積は、\(xyz\)の3次元空間で登場してくる概念です。
例えば、\(xy\)平面内に\(\vec{ a }\)と\(\vec{ b }\)が与えられているとき、この2つのベクトルの外積\(\vec{ a }\times\vec{ b }\)は図のように\(z\)軸方向の\(\vec{ c }\)と計算されます。計算は内積以上にかなり面倒ですので省略しますが、計算結果はベクトル量になります。
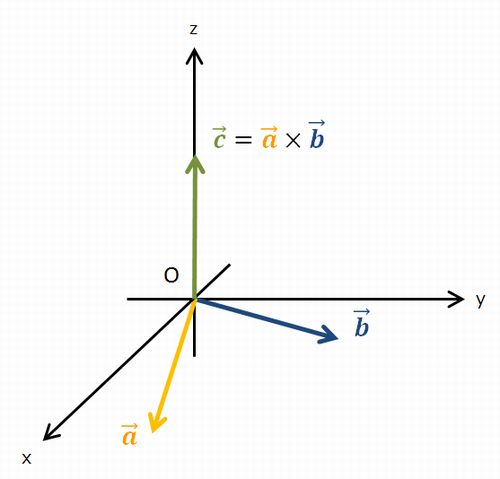
ここでの重要なポイントとしては、
- \(\vec{ c }\)の向きは\(\vec{ a }\)から\(\vec{ b }\)の向きに右ねじを回したときにねじの進む向きであり、
- その大きさは\(\vec{ a }\)と\(\vec{ b }\)からなる平行四辺形の面積と同じになる
ということです。
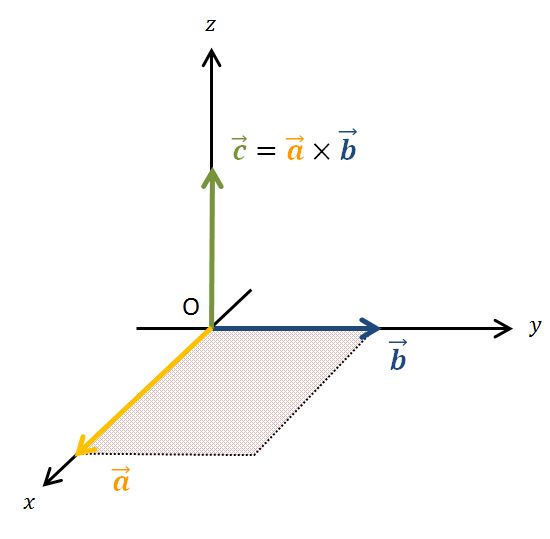
ここでやっと「右ねじの法則」が登場してきます!!ここが今回の記事の最大のポイントです。
平行四辺形の面積は求めるのが面倒ですが、\(\vec{ a }\)と\(\vec{ b }\)が直交している場合は話が簡単になります。
上図の場合は、\(\vec{ c }\)の大きさは\(|\vec{ a }||\vec{ b }|\)となります。
長々と内積・外積について説明してきましたが
外積のベクトル関係を表した図はどこかで見たことありませんか?
そうです、電磁気学の公式は実は外積表記だったものをスカラー表記したものです。
\(F=qvB\) は実は \(\vec{F}=q\vec{v}\times\vec{B}\)
電験で有名な\(F=qvB\)を例に、この公式を外積の表記に戻す方法を説明していきます。
\(F=qvB\)のうち、ベクトル量(方向のある量)は力\(F\)と速度\(v\)と磁束密度\(B\)ですので、これらをベクトルに戻してベクトルとベクトルの間には「\(\times\)」を挿入します。
ということで、\(F=qvB\)は
\begin{align}\vec{F}=q\vec{v}\times\vec{B}\\ \end{align}
となります。
また、\(\vec{F}\)の向きは\(\vec{ v }\)から\(\vec{ B }\)の向きに右ねじを回したときにねじの進む向きとなります。
私は毎回シャーペンを使って、試験会場で\(\vec{v}\)の向きから\(\vec{B}\)の向きに回す操作をしています笑 そして、回したときに右ねじがどう進むのかを想像しています。
ここで注意してほしいのは、文字の順番です。順番を間違うとベクトルの向きが逆転してしまうので、外積を意識した順番で覚えてください。ちなみに、スカラー量(定数倍)の式内の位置はどこでも構いません。
その他の公式は?
ということで、電験の参考書に乗っている範囲の公式は、↓の順番で覚えてはいかがでしょうか。
あとはこれら公式を呪詛のごとく呟いて覚えるだけです笑
私の場合は高校生の時から呟いていたので、電験が終わって1年たった今でもこれらの公式はスムーズに出てきますね笑
\(\vec{ a }\)と\(\vec{ b }\)のなす角\(\sin\theta\)が設定されているときもある
電験の問題では\(\vec{ a }\)と\(\vec{ b }\)のなす角\(\sin\theta\)が登場してくるときがあります。
そういうときは、
\begin{align}c=ab\sin\theta\\ \end{align}
と計算するわけですが、外積の概念に基づいてこの辺りを少し詳しく説明してみます。
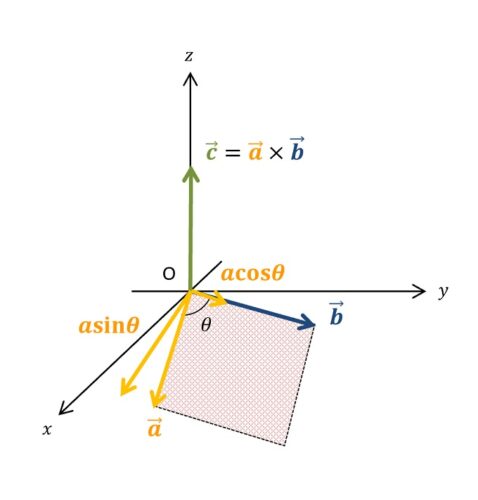
\(\vec{ b }\)に平行な\(\vec{ a }\)の成分(\(a\cos\theta\))は、\(\vec{ b }\)に向かってこれ以上右ねじの向きに回せないので、\(\vec{ c }\)の大きさに貢献しません。
一方で、\(\vec{ b }\)に垂直な\(\vec{ a }\)の成分(\(a\sin\theta\))のみが\(\vec{ b }\)に向かって右ねじの向きに回すことができ、\(\vec{ c }\)の大きさに貢献します。
しかも、その大きさは長方形の大きさと等しく、
\begin{align}c=ab\sin\theta\\ \end{align}
となります。
もう少し数学的な見方
平行四辺形の面積を\(ab\sin\theta\)と計算している、と解釈しても間違いではありません。
まとめ
ベクトルの外積(右ねじの法則)という新たな概念を使えば、今回のようにベクトルの向きまでまとめて1つの方法で対処することができます。
これをそっくり覚えてしまえば、電流の流れる向きと磁場の向きから、フレミングの左手の法則を使わずに電磁力の向きがわかるようになります。
外積の計算は非常に面倒ですので、覚えなくていいです。というか、電験で外積のベクトル計算なんて出ていきません笑
コチラのサイトで詳しい計算が紹介されていましたので、どうしても知りたい方はそちらをご覧になってください。
単純暗記は省エネしてやっていきましょう!
それでは次回!














最後の図、asinθとacosθ逆じゃないですか?もし合っていたら申し訳ありません。
>ただの高3さん
コメントありがとうございます。
確かに間違っておりましたので修正しました。
ご指摘ありがとうございました。