皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
以前の記事で計算を省略していたところを、少し丁寧に解説してみます。
そこでは「専門書をご確認して下さい」としていましたが、ラプラス変換の専門書は普通の本屋においていないことが多く、実際に本屋に行っても無駄足になる可能性があると思い、記載してみました。
ですので、今回はいつにも増して数学的な記事になります。面白みは、、、ありません笑
前回計算を省略していた式

以前の記事で説明していたラプラス変換式は以下の3つとなります。
\begin{align}\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} E \mathrm{d}t&=\frac{E}{s}\\
\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} \left[ L\frac{\mathrm{d}i}{\mathrm{d}t}\right] \mathrm{d}t&=LsI(s)\\
\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} \frac{1}{C}\left[ \displaystyle \int_{0}^{ t } i\mathrm{d}t\right] \mathrm{d}t&=\frac{I(s)}{Cs}\\
\end{align}
定電源のラプラス変換
\(\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} E \mathrm{d}t\)について、\(\displaystyle \int\)の中の\(s\)は定数として扱えて、これを部分積分すると
\begin{align}\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} E \mathrm{d}t &=\left[ \frac{1}{-s}\mathrm{e}^{-st}E \right] _{0}^{ \infty }-\displaystyle \int_{0}^{ \infty } \left( \frac{1}{-s}\mathrm{e}^{-st}\times 0 \right) \mathrm{d}t\\
&=\frac{E}{s}\\
\end{align}
となります。
コイル部分のラプラス変換
これも部分積分を使用します。
\(\frac{\mathrm{d}i}{\mathrm{d}t}\)を\(t\)で積分すると\(i\)に戻ることに注意して、
\begin{align}\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} \left[ L\frac{\mathrm{d}i}{\mathrm{d}t} \right] \mathrm{d}t&=L{[\mathrm{e}^{-st}i]_{0}^{ \infty }-\displaystyle \int_{0}^{ \infty }(-s)\mathrm{e}^{-st}i\mathrm{d}t}\\
&=L{-i(0)+sI(s)}\\
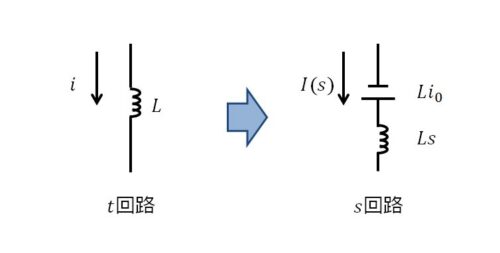
&=LsI(s)-Li(0)\quad …(1)\\
\end{align}
初期条件が登場…
以前の記事では特に初期条件に言及していなく、暗黙の内に\(\boldsymbol{ i(0)=0}\)としていました。しかし過去問では、初期条件として\(t=0\)で既に電流が流れていたりします。この初期条件をラプラス変換に盛り込むと、式(1)のようになります。
つまり、\(LsI(s)\)を電圧降下する方向で考えると、\(\boldsymbol{ Li(0) }\)は電圧上昇する方向に電圧素子として表記されることになります。
コンデンサ部分のラプラス変換
コイルのときと同様に全体の部分積分をする前に、合成関数の微分をしていきます。
詳しいことは省略しますが、微分は分数のように扱えるので、
\begin{align}\mathrm{e}^{-st}\mathrm{d}t&=\frac{\mathrm{e}^{-st}\mathrm{d}t}{\mathrm{d}\mathrm{e}^{-st}}\mathrm{d}\mathrm{e}^{-st}\\
&=\frac{ \mathrm{e}^{-st} }{\frac{\mathrm{d}\mathrm{e}^{-st}}{\mathrm{d}t}}\mathrm{d}\mathrm{e}^{-st}\\
&=\frac{\mathrm{e}^{-st}}{-s\mathrm{e}^{-st}}\mathrm{d}\mathrm{e}^{-st}\\
&=\frac{\mathrm{d}\mathrm{e}^{-st}}{-s}\\
\end{align}
となります。これを使うと、
\begin{align}\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} \frac{1}{C}\left[ \displaystyle \int_{0}^{ t } i\mathrm{d}t\right] \mathrm{d}t&=\frac{1}{C}\displaystyle \int_{0}^{ \infty }\left[ \displaystyle \int_{0}^{ t } i\mathrm{d}t \right] \frac{\mathrm{d}\mathrm{e}^{-st}}{-s}\\
&=\frac{1}{C}\left(\left[\displaystyle \int_{0}^{ t } i\mathrm{d}t\times\frac{\mathrm{e}^{-st}}{-s}\right]_{0}^{ \infty }-\displaystyle \int_{0}^{ \infty } i\frac{\mathrm{e}^{-st}}{-s}\mathrm{d}\right)\\
&=-\frac{1}{Cs}\left[\displaystyle \int_{0}^{ t } i\mathrm{d}t\times\mathrm{e}^{-st}\right]_{0}^{ \infty }+\frac{1}{Cs}\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} i \mathrm{d}t …(2)\\
\end{align}
となります。
ここで、
\begin{align}\left[\displaystyle \int_{0}^{ t } i\mathrm{d}t\times\mathrm{e}^{-st}\right]_{0}^{ \infty }&=\displaystyle \int_{0}^{ \infty } i\mathrm{d}t\times\mathrm{e}^{-\infty}- \displaystyle \int_{0}^{ 0 } i\mathrm{d}t\times\mathrm{e}^{0}\\
&=0-0\\
&=0\end{align}
となります。
また、定義通り
\begin{align}\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} i(t) \mathrm{d}t \equiv I(s)\\ \end{align}
となります。
これらを式(2)に代入して、
\begin{align}\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} \frac{1}{C}\left[ \displaystyle \int_{0}^{ t } i\mathrm{d}t\right] \mathrm{d}t=\frac{I(s)}{Cs}\\ \end{align}
となります。
初期条件は意図的に紛れ込ませる
コイルのときと違って、コンデンサの計算では意図的に初期条件を組み込まないと、ラプラス変換後に初期条件が現れてきません。
どういうことかというと、
\begin{align}\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} \frac{1}{C}\left[ \displaystyle \int_{0}^{ t } i\mathrm{d}t\right] \mathrm{d}t\\ \end{align}
に初期電荷\(Q_0\)を
\begin{align}\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} \frac{1}{C}\left[ \displaystyle \int_{0}^{ t } i\mathrm{d}t + Q_0 \right] \mathrm{d}t\\ \end{align}
と紛れ込ませます。
これを計算していくと、
\begin{align}\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} \frac{1}{C}\left[ \displaystyle \int_{0}^{ t } i\mathrm{d}t + Q_0 \right] \mathrm{d}t&=\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} \frac{1}{C}\left[ \displaystyle \int_{0}^{ t } i\mathrm{d}t\right] \mathrm{d}t+\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} \frac{Q_0}{C}\mathrm{d}t \\
&=\frac{I(s)}{Cs}+ \frac{Q_0}{C}\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st}\mathrm{d}t …(3)\\
\end{align}
となります。
ここで、
\begin{align}\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st}\mathrm{d}t&=\left[ \frac{1}{-s}\mathrm{e}^{-st}\right] _{0}^{ \infty }\\
&=\frac{1}{s}\\ \end{align}
となるので、式(3)に代入すると
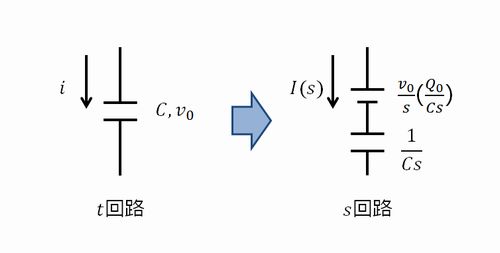
\begin{align}\displaystyle \int_{0}^{ \infty }\mathrm{e}^{-st} \frac{1}{C}\left[ \displaystyle \int_{0}^{ t } i\mathrm{d}t + Q_0 \right] \mathrm{d}t&=\frac{I(s)}{Cs}+ \frac{Q_0}{Cs}\\
\end{align}
となります。
\end{align}
となります。
つまり、\(\frac{I(s)}{Cs}\)を電圧降下する方向で考えると、\(\boldsymbol{ \frac{Q_0}{Cs} }\)も電圧降下する方向に電圧素子として表記されることになります。
まとめ
今回は部分積分尽くしの記事となり、右(微分)を見ながら左(積分)を見るような内容となってしまいました。
結構混乱する内容でしたが、
\begin{align}Ls \longleftrightarrow \omega L, \frac{1}{Cs}\longleftrightarrow \frac{1}{\omega C}\\ \end{align}
と交流回路のインピーダンスと対応して覚えてしまえば単純です。
それでは次回!