共役を感覚的に使い分けて複素電力を求めてみよう

皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。

専門用語ばかりのタイトルになってしまい、何についての記事を私が書こうとしているのか読者の皆さまを混乱させてしまったかと思います笑

今回書こうとしているお話は、皮相電力を複素数で表す方法、つまり複素電力

\begin{align}
\dot{S}&=\overline{\dot{V}}\dot{I}\\
&=P+\mathrm{j}Q\\
\end{align}

\begin{align}
\dot{S}&=\dot{V}\overline{\dot{I}}\\
&=P+\mathrm{j}Q\\
\end{align}

という式のどちらかを問題文に合わせて感覚的に立てる方法についてです。

ケンタ

今回はエネルギー管理士以降に必要となってくる知識についての独自解釈となります。

今回紹介する内容は、勉強していた時に手持ちの参考書に詳しく載っていなかったため、苦肉の策で独自に編み出した導出方法です。が、電験１種まで矛盾なく使えていましたので、そこそこ信憑性はあると思います笑

なお、今回の説明には

を肌感覚で使えていることが前提にあります。前提と言っても、ある程度補足を入れながら説明していきますので、取り敢えず読み進めていって問題はありません。

パターン１：進相条件

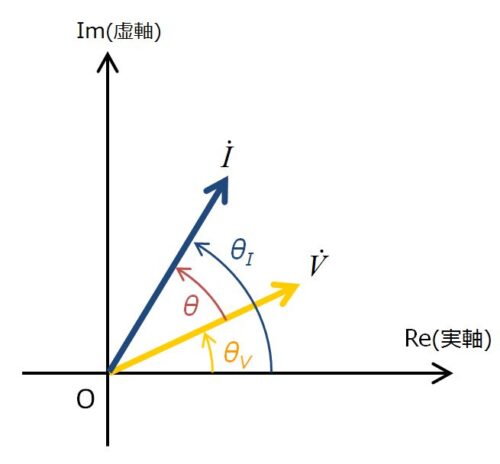
上図のように電圧\(\dot{V}\)と電流\(\dot{I}\)があったとき、\(\dot{I}\)の方が\(\dot{V}\)の反時計方向に位置していますので、進相条件にあると言えます。

このようなときは\(\overline{\dot{V}}\dot{I}\)を使って皮相電力を計算します。\(\dot{V}\overline{\dot{I}}\)と迷ったら、位相差を作れる方を選びましょう。なぜ\(\overline{\dot{V}}\dot{I}\)が位相差を作れるかは、フェーザ表示で計算していくと分かります。

\begin{align}
\overline{\dot{V}}\dot{I}&=V\angle (-\theta_\mathrm{V}) \times I\angle \theta_\mathrm{I}\\
&=VI\angle (\theta_\mathrm{I}-\theta_\mathrm{V})\\
&=VI\angle \theta\\
\end{align}

ということで、位相差\(\theta\)を作れます。

続けると

\begin{align}
VI\angle \theta&=VI(\cos\theta+\mathrm{j}\sin\theta)\\
&=P+\mathrm{j}Q\\
\end{align}

となります。

つまり、

\begin{align}
\dot{S}&=\overline{\dot{V}}\dot{I}\\
&=P+\mathrm{j}Q\\
\end{align}

となります。

ここで、図に戻ってみます。この図は進相条件ですので、上式でいう無効電力\(Q\)は進相が正となります。

複素計算をした結果、虚部が負となった場合は、遅相無効電力が発生していることになります。つまり、そもそもは遅相条件だったということです。

パターン２：遅相条件

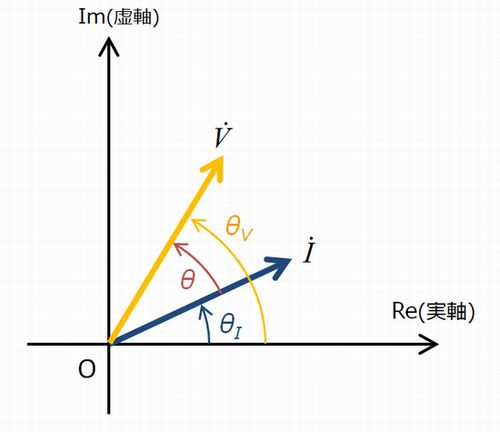
次は、上図のような遅相条件にあるときです。\(\theta_\mathrm{V}-\theta_\mathrm{I}\)となるように共役を作っていきます。

\begin{align}
\dot{V}\overline{\dot{I}}&=V\angle \theta_\mathrm{V} \times I\angle (-\theta_\mathrm{I})\\
&=VI\angle (\theta_\mathrm{V}-\theta_\mathrm{I})\\
&=VI\angle \theta\\
&=VI(\cos\theta+\mathrm{j}\sin\theta)\\
&=P+\mathrm{j}Q\\
\end{align}

つまり、

\begin{align}
\dot{S}&=\dot{V}\overline{\dot{I}}\\
&=P+\mathrm{j}Q\\
\end{align}

となります。

ここで、図に戻ってみます。この図は遅相条件ですので、上式でいう無効電力\(Q\)は遅相が正となります。

複素計算をした結果、虚部が負となった場合は進相無効電力が発生していることになります。つまり、そもそもは進相条件だったということです。

例題で実際に解いてみましょう

\begin{align}
\dot{V}&=5+\mathrm{j}2[\mathrm{V}]\\
\dot{I}&=3+\mathrm{j}[\mathrm{A}]\\
\end{align}

と与えられていたとき、

\begin{align}
\overline{\dot{V}}\dot{I}&=(5-\mathrm{j}2)(3+\mathrm{j})\\
&=17-\mathrm{j}\\
\end{align}

となりますので、有効電力は\(17\mathrm{W}\)、虚部は負値であるため遅相無効電力であり、その大きさは\(1\mathrm{var}\)となります。

念のため、もう一方の式で計算してみても

\begin{align}
\dot{V}\overline{\dot{I}}&=(5+\mathrm{j}2)(3-\mathrm{j})\\
&=17+\mathrm{j}\\
\end{align}

となり、やはり同じ結果になります。

無駄なテクニック：進相・遅相条件のみの判断

実は進相か遅相かの判断だけであれば、図からの導出→複素計算という手順を踏まずにできます。

電圧の実部に合わせるように電流の実部を実数倍してみると、

\begin{align}
\frac{5}{3}\dot{I}&=5+\mathrm{j}\frac{5}{3}\mathrm{A}\\
\end{align}

となります。

この虚部は電圧の虚部より小さいため、電流は電圧のベクトルより下側に来ていることが分かります。つまり、今回は遅相条件ということが分かります。

電験２種以降ではどのように出題されるのか

実は、電験２種以降では\(\overline{\dot{V}}\dot{I}\)または\(\dot{V}\overline{\dot{I}}\)の複素計算をさせるような問題は出てきません(?!)

エネルギー管理士では、平成27年度課目Ⅱの問題4(1)に出題されていましたが、このような計算は電験２種以降では稀です。

電験２種以降でよくある出題としては、文字または数字で与えられている\(P\)と\(Q\)を使用して、\(\dot{I}\)を求める方法です。つまり、公式の逆手を取る方法です。

ケース１

進相条件、つまり\(Q\)を正の進相無効電力とすると

\begin{align}
\overline{\dot{V_\mathrm{r}}}\dot{I_\mathrm{r}}&=P+\mathrm{j}Q\\
\dot{I_\mathrm{r}}&=\frac{P+\mathrm{j}Q}{\overline{\dot{V_\mathrm{r}}}}\\
\end{align}

大抵の場合、\(\dot{V_\mathrm{r}}\)をベクトルの基準としますので、

\begin{align}
\dot{V}&=V\angle 0^{ \circ }\\
&=V\\
\end{align}

となり、共役しても値が変わりません。つまり、

\begin{align}
\dot{I}&=\frac{P+\mathrm{j}Q}{V}\
\end{align}

で、\(\dot{I}\)を計算することができます。この式に遅相無効電力を代入したい場合は負値として\(Q\)に代入します。そうすれば、\(\dot{I}\)も虚部は負値となるので、電流が電圧より遅れていることと一致します。

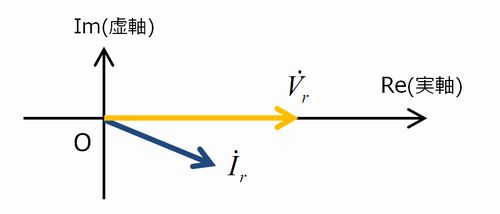
↑のようなベクトル関係になります。

ケース２

遅相条件、つまり\(Q\)を正の遅相無効電力とすると

\begin{align}
\dot{V_\mathrm{r}}\overline{\dot{I_\mathrm{r}}}&=P+\mathrm{j}Q\\
\overline{\dot{I_\mathrm{r}}}&=\frac{P+\mathrm{j}Q}{\dot{V_\mathrm{r}}}\\
\dot{I_\mathrm{r}}&=\frac{P-\mathrm{j}Q}{\overline{\dot{V_\mathrm{r}}}}\\
\end{align}

となります。厳密に説明すると、最後の行では分子だけでなく分母の\(\mathrm{j}\)の符号も反転します。しかしケース1と同様に、大抵の場合\(\dot{V_\mathrm{r}}\)をベクトルの基準としますので、

\begin{align}
\dot{I_\mathrm{r}}&=\frac{P-\mathrm{j}Q}{V_\mathrm{r}}\\
\end{align}

で計算してしまいます。この式に遅相無効電力を代入したい場合は正値として\(Q\)に代入します。そうすれば、\(\dot{I}\)も虚部は負値となるので、電流が電圧より遅れていることと一致します。

まとめ：結局どちらの公式を使えば良いのか

進相条件だから…とか、遅相条件だから…とか延々と書いてきましたが、結局のところは負値を使えば最終的に対応できるので、好きな方を使って問題ないです。

個人的な好みとしては、送電問題では電流が遅れることが多いので、遅相条件の式をよく使っていました。でも、本当にどちらでも構わないです。気を付けておいてほしいのは、ど忘れしたときのために今回の導出をできるようにおくことだけです。

もちろん、暗記してしまう方が楽だと感じた方はソチラの方で良いでしょうが、電験２種とかになってくると暗記のメモリは論述問題に取っておいた方が良いのかなと思っています。

それでは次回！