皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
少し前に風力発電に関する独自解釈の記事を書きました。

今回はその続編を書いてみます。
風速→風量だと?

前回は風速と出力の関係を説明していました。一方で、風速と似た単語で「風量」というものもあります。
風量は風速と概念的に似ていますので、出力は風量の3乗に比例するのかどうかは気になるところです。前回と同じように導出してみます。
導出
前回と同様に運動エネルギー\(\frac{1}{2}mv^2\)を使いますので、風が流れるときの知りたい量としては質量と速度です。これらの量を風量\(\boldsymbol{V}\mathrm{[m^3/s]}\)を使って設定していきます。
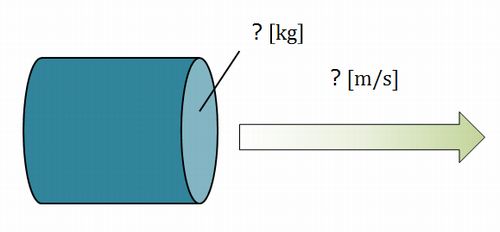
体積は風量\(V\mathrm{[m^3/s]}\)、吹く時間\(\Delta t\mathrm{[s]}\)、空気の密度\(\rho\mathrm{[kg/m^3]}\)を使って\(\rho V\Delta t[\mathrm{kg}]\)と表せます。
速度は風量\(V\mathrm{[m^3/s]}\)、断面積\(S\mathrm{[m^2]}\)を使って\(\frac{V}{S}\mathrm{[m/s]}\)と表せます。
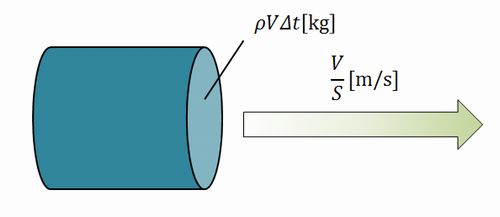
あとは運動エネルギー\(E\)に代入していき
\begin{align}
E&=\frac{1}{2}mv^2\\
&=\frac{1}{2}\rho V\Delta t\times (\frac{V}{S})^2\\
&=\frac{\rho \Delta tV^3}{2S^2}\\
\end{align}
となります。出力\(P\)は単位時間あたりのエネルギー\(E\)ですので、
\begin{align}
P&=\frac{E}{\Delta t}\\
&=\frac{\rho V^3}{2S^2}\\
&\propto V^3\\
\end{align}
つまり、出力は流量の3乗にも比例することになります。
もう少しお手軽な導出方法

流量についても速度のときと同様に根本からの導出をしましたが、「出力が速度の3乗に比例する」ということを覚えていれば、流量の導出はもう少し簡単に済む方法があります。
速度\(v\)と流量\(V\)には
\begin{align}v=\frac{V}{S}\ \end{align}
の関係があるので、
\begin{align}
P&\propto v^3\\
&=\left(\frac{V}{S}\right)^3\\
&\propto V^3\\
\end{align}
と変形できます。
\(\propto\)と\(=\)が入り混じった式変形となります。
\begin{align}\left(\frac{V}{S}\right)^3\propto V^3\end{align}のところは詳しく書くと
\begin{align}\left(\frac{V}{S}\right)^3=\frac{1}{S^3}\times V^3\propto V^3 \end{align}となります。\(\frac{1}{S^3}\)を定数としています。
まとめ
前回に引き続き今回も風力発電を例に「~の3乗に比例する」というのを説明していきましたが、電験の選択肢問題には「~に比例する」、「~の2乗に反比例する」といったものもあります。
その背景にある計算を自分で調べる習慣を是非つけてみてください。自身の知っている公式同士が繋がって、より忘れにくくなる副次効果もあります。
それでは次回!