皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
電験まであと22日ですね。最後のスパートをかけている時期だと思います。
お盆で遊びたくなったり、帰省したくなったりするかもしれませんが、今年で最後の夏にする!という意気込みでがんばってください。
今日はコンボイさんから質問のありました、タイトルの解説を行いたいと思います。
というのも、過去問再挑戦シリーズの一番初めの電験3種理論の問15について、私が「正攻法でないが何とか解けた」的なコメントをしまして、それに対して読者の方から解説を依頼されました。
今回はその説明となります。
電験3種 理論 平成28年 問15
自己流で解いた部分は(1)ですので、(2)は今回は割愛します。
さて、問題はコチラです。(⇒模範解答)
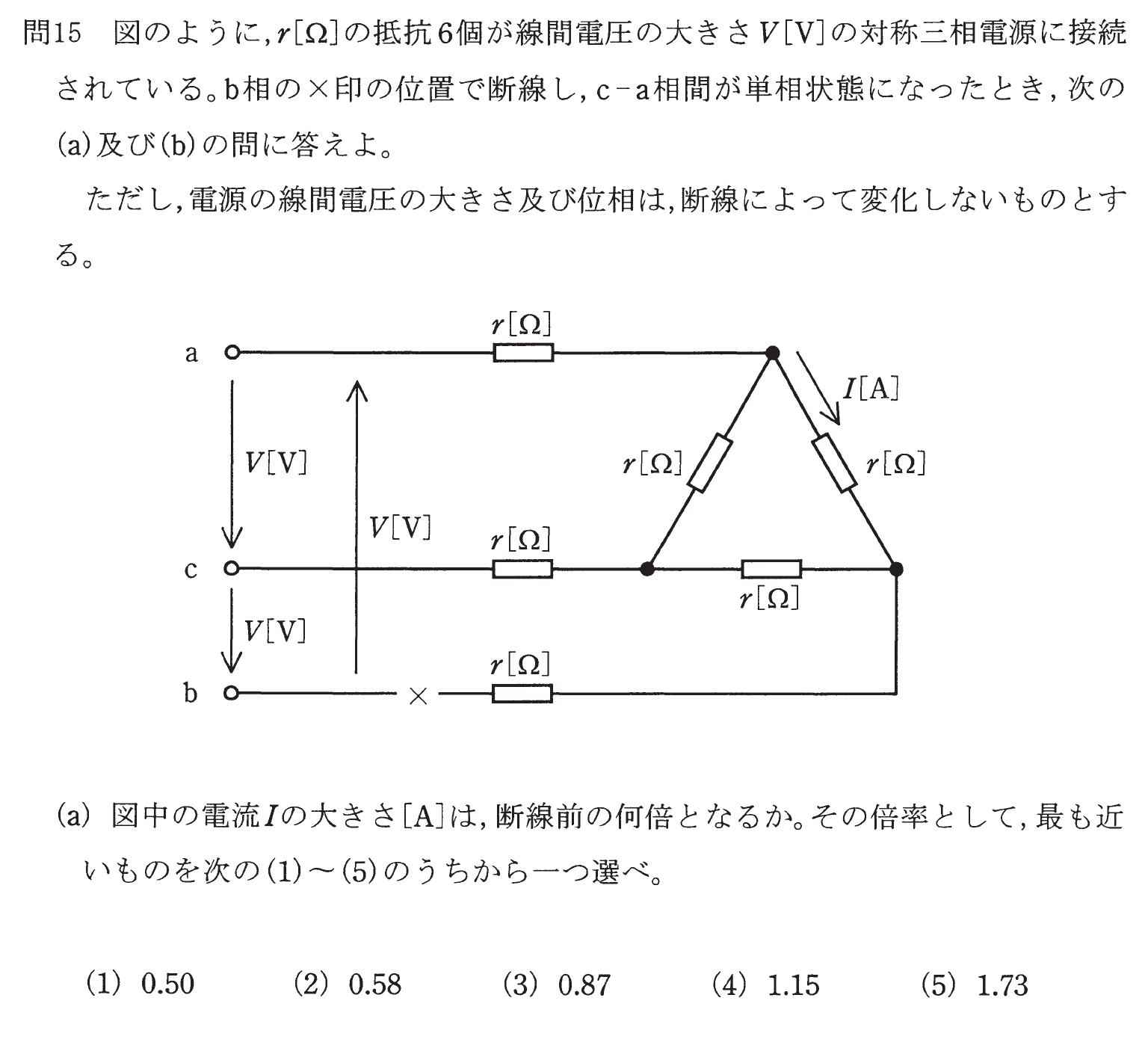
この問題を読んだとき、
- 断線前は普通の三相回路だから、電流はすぐ計算できるし
- 断線後は単相回路だから、この時の電流もすぐ計算できるし
と思っていたのですが、解き始めると初っ端から躓きました。
⊿の前にも抵抗が有るので、これでは⊿部分を一度Yにして、線電流を計算する必要があります。(模範解答ではそうなっています。)
ただ、この時の私は線電流を相電流に変換する際に\(\sqrt{3}\)倍にすればいいのか、\(\frac{1}{\sqrt{3}}\)倍にすればいいのか思い出せなかったので、別の解法を選んだわけです。
(自己流)解法の解説
先ず、事故電流\(I\)の計算は模範解答と同じように求めて\(\frac{V}{8r}\)となります。
次に、正常時の相電流を求めるために、模範解答と同様に線電流\(I’\)を求めます。
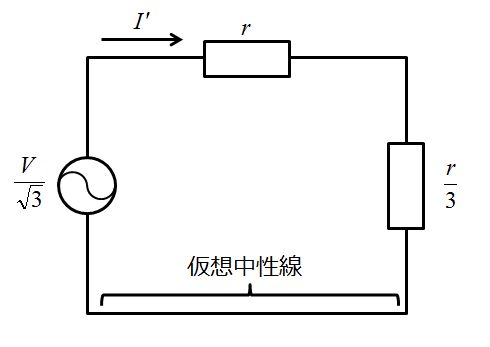
計算を省略しますが、
\begin{align}I’&=\frac{\sqrt{3}V}{4r}\\ \end{align}
となります。
ここからが自己流です。
この線電流を利用して、⊿に突入する前の相電圧を求めます。(図のオレンジ色の電圧です。)
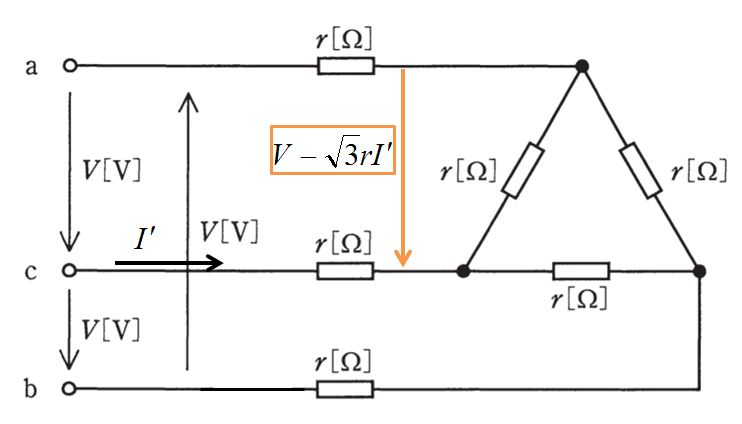
そうです。ここで電圧降下定数\(\sqrt{3}\)が出てきます。
⊿に突入する前の電圧は
\begin{align}V-\sqrt{3}rI’&=V-\sqrt{3}r\times\frac{\sqrt{3}V}{4r}\\
&=\frac{V}{4}\\ \end{align}
となります。
よって、正常時の相電流\(I^{\prime\prime}\)は
\begin{align}I^{\prime\prime}&=\frac{\frac{V}{4}}{r}\\
&=\frac{V}{4r}\\ \end{align}
となり、(a)の答えは
\begin{align}\frac{I}{I^{\prime\prime}}&=\frac{\frac{V}{8r}}{\frac{V}{4r}}\\
&=0.5\\ \end{align}
となります。
遠回りの回答となりましたが、一応この方法でも正解となります。
そもそも
そもそも線電流と相電流の比率を覚えておくなり、時間に余裕があったので導出するなりしておけば良かったんですよね笑
当時は、理論の試験時間が60分と勘違いして急いで解いていたから、仕方ないといえば仕方ないのですが。
ということで、自分の備忘録的にも読者の方のためにも(?)、次回は私が「線電流が相電流に対して大きさと位相がどうなっているか」を思い出すときの導出方法をご紹介します。導出自体は3分もあれば終わるくらいの計算量です。
まとめ
今回迂回した解法をとってしまった教訓は、単純に「線電流と相電流の関係を覚えておけ」ということですね笑
試験会場で不覚に陥った場合でも、いくつか周辺知識を知っているとそれらを組合せてなんとかなることが多々あります。今回は何とかなった場合のお話でしたが、試験というものは時の運ですので、分からない問題に出くわしたときは組合せで解答までたどり着けたらラッキーくらいに思うようにしています。
こういったことでボーダーラインを越えてしまえば官軍ですね!
それでは次回!













