意外と陥りがち？！式展開のワナ

皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。

電験と数学は切っても切れない関係にあります。

四則計算に始まり三角比、複素数、微積分…　公式を覚えればある程度の計算の筋道を立てることができるものの、四則計算に限っては何パターンか解き方が存在するので、その時々にどのパターンを選ぶかということは数学センスによるものが大きいです。

数学センスと一言で言い切ってしまえば簡単ですが、解説する側にとっては中々説明しにくい部分でもあるため、きちんとした方法というか、周りくどくない方法を選ぶ能力を身に付けにくい構造があるのではないかと思います。

ベストな数学参考書

この辺りの能力を磨けるような参考書を紹介できればなと思い探してみましたが、案の定見つけることができませんでした。電験の数学参考書だけでなく、高校数学の参考書まで対象を広げで探してみましたが、どの参考書も個別（三角比、複素数、ベクトルなど）の解説をしはするものの、四則演算に重きを置いた解説をしている章は存在しなかったです。

色々考えてみた結果、色んな形の膨大な計算をするしかないのか？という結論に至りました。（結論と言いながら？が付いています笑）

四則演算というのは、当たり前ですが数学の色んな分野に散らばって存在しています。しかし、その分野ごとに行う「計算の型」的なものは存在しますので、型を覚えていくうちに、ひいてはある式に対しての四則演算の周りくどくない方法を体で覚えていくのだろうと推測します。その洗練された能力的なものは人によって千差万別ですので、やはり教える側は伝えることが難しいのだと思います。

【電験２種】管理人がお勧めする数学の参考書皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。 6月に入り試験がだんだん間近に迫ってきましたね。 この時...

なんでこんな話をしているのかというと

とあるWebサイトで、とても周りくどい式展開をしていたからです。

そのページでは繁分数を含む

\begin{align}\frac{E}{R_1+\frac{R_2R_x}{R_2+R_x}}\times\frac{R_2}{R_2+R_x}\\ \end{align}

の式展開の解説をしていました。文章での解説は端折りますが、式展開自体は以下の通りになります。

\begin{align}
&\frac{E}{R_1+\frac{R_2R_x}{R_2+R_x}}\times\frac{R_2}{R_2+R_x}\\
&=\frac{E}{\frac{R_1(R_2+R_x)+R_2R_x}{R_2+R_x}}\times\frac{R_2}{R_2+R_x}\\
&=\frac{E(R_2+R_x)}{R_1(R_2+R_x)+R_2R_x}\times\frac{R_2}{R_2+R_x}\\
&=\frac{E}{R_1(R_2+R_x)+R_2R_x}\times R_2\\
&=\frac{R_2}{R_1(R_2+R_x)+R_2R_x}\times E\\
\end{align}

私が解くなら

私はこの式展開を暗算で、しかも5秒でできます。

繁分数の定石は確かに複雑なところを解きほぐすことですが、解きほぐす前に1つ確認しておくとすんなり解けることが多いです。それは分母間の計算を先にするとどうなるかです。

今回は以下の2ヶ所が同じ形ですので、分配法則を使って分母の中の分数を解消することができます。

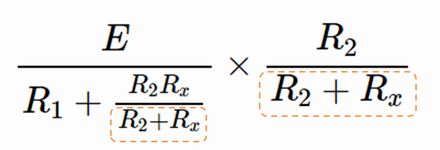
つまり、

\begin{align}
&\frac{E}{R_1+\frac{R_2R_x}{R_2+R_x}}\times\frac{R_2}{R_2+R_x}\\
&=\frac{ER_2}{R_1\times(R_2+R_x)+\frac{R_2R_x}{R_2+R_x}\times(R_2+R_x)}\\
&=\frac{R_2}{R_1(R_2+R_x)+R_2R_x}\times E\\
\end{align}

といった具合にです。

ちなみに、私ならもう少し先まで展開します。

\begin{align}\frac{R_2}{R_1R_2+R_2R_x+R_xR_1}\times E\\ \end{align}

までです。

このときの、1→2→x→1で1周して表記するのを、数学では「円環の順」と言います。

まぁ見た目が綺麗ってだけですね笑　電気?では円環の部分をΔ(デルタ)で代替表記することがあります。

\begin{align}\frac{R_2}{\Delta}\times E\\ \end{align}

といった具合にです。これはこれでさっぱりしますね。

まとめ

簡便な計算方法は自分で見つけるか、他者のやり方を見るかのどちらかしかありません。そういった事情がありますので、計算が楽になる自分の癖に気づけば、これからも紹介していきます！

恐らく自覚していないだけで、他にも紹介できる方法があると思いますので、時間があるときに参考書を読み返してみようと思います。

ちなみに、数学の参考書を探しに行ったときに、前回記事の↓の本を見つけてきました笑

電験辞書の決定版（仮）皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。 電験という未知の分野を勉強していると、このキーワードってど...

思いがけない収穫をしてきたものです笑

それでは次回！