皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
Twitterや2chでは合格・不合格の阿鼻叫喚となっていますね。
土日の試験問題と解答が既に試験センターでアップされていますので、私も見る気になれば見れます。が、翔泳社が試験解説を今月中に行うという情報を仕入れましたので、私の出る幕はないかと思います。餅はより美味しい餅屋に、ということですね笑
(翔泳社の解説を見た上でわからないところがありましたらコメント下さい。私なりに調べて噛み砕いて解説してみます。こうやって書いていると翔泳社の方に怒られますかね汗)
さて、今回は前回に引き続き「過渡現象」です。
内容的に今回で書きたいのを出し切りそうなので、今回が完結編となります。
ラプラス変換とは
ラプラス変換は電験1・2種二次試験の制御問題で頻出の計算手法です。
モーターの出力制御などは感覚的には時間領域\(t\)の話ですが、
- ラプラス変換をして\(s\)空間に話を持っていき、
- \(s\)空間の中で計算をして1度答えを出し、
- 時間領域(\(t\)空間と言います)に戻して\(t\)の答えを出す
というようなことをしています。
なぜ、\(t\)空間の中でそのまま計算をしないのかというと、答えは簡単、計算が面倒くさいからです。

どのくらい面倒なのか
\(t\)空間の中でそのまま計算をする場合は、微分方程式を解く必要があります。
対して、\(s\)空間の中では、\(t\)空間で2階の微分方程式だった場合は、2次方程式を解くだけです。
どれだけ簡単かは一目瞭然ですね。
このように微分方程式を使うときは、同時にラプラス変換も覚えておくと時間の省略ができます。感の良い方なら察し始めているでしょうが、微分方程式を使う過渡現象でもラプラス変換を使うと計算がかなり簡単になります。
RLC直並列回路で例題
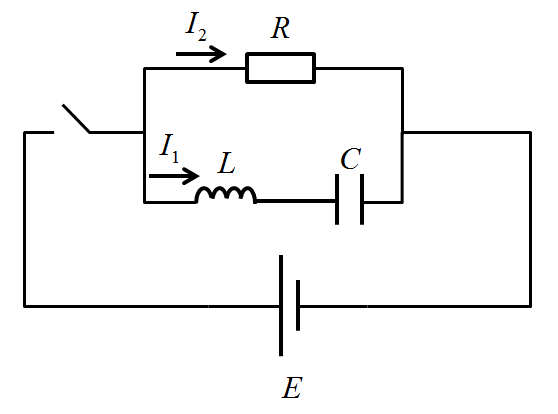
前回の記事ではこの微分方程式を
\begin{align}L\frac{\mathrm{d}I_1}{\mathrm{d}t}+\frac{1}{C}\int I_1\mathrm{d}t&=RI_2=E\\ \end{align}
と説明しました。
この式をきちんとラプラス変換をすると、
\begin{align}\frac{1}{Cs}I_1(s)+LsI_1(s)&=RI_2(s)=\frac{E}{s}\\ \end{align}
となります。

このやり方ですと、一度微分方程式を立てなければならないので、結構めんどくさいです。
私の場合は、\(s\)回路を作ってから、それについてオームの法則に代入していきます。
どういうことかといいますと、先ず一度図を書き換えます。
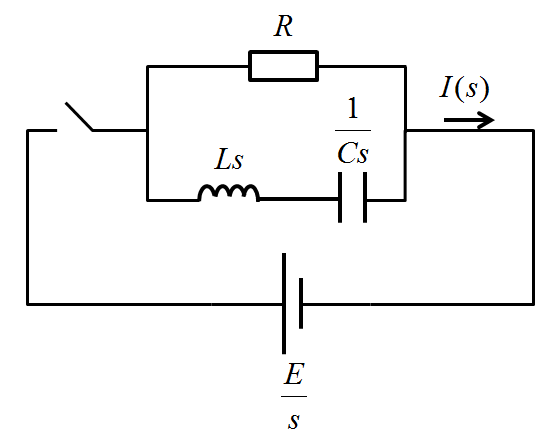
次に、交流回路のように式を立てます。
\begin{align}I(s)\times\frac{(\frac{1}{Cs}+Ls)R}{(\frac{1}{Cs}+Ls)+R}&=\frac{E}{s}\\ \end{align}
あとは解いて終わりです。(下の方のおまけで最後まで計算します。)
まとめ
苦手意識を持っている人が多い過渡現象でも、ラプラス変換を知っていると微分方程式ほどではない計算量で済みます。
どちらも同じくらい面倒と感じるかもしれませんが、(パワエレを選ばない限り)ラプラス変換は2次試験で必須ですので、微分方程式の複数の解法を新たに覚えるよりかは幾分楽かと思います。
というか、私は一次試験理論の過渡現象のところでラプラス変換をマスターしました。ですので、二次試験の機械・制御の準備では、同期機・誘導機・変圧器の問題に集中することができていました。(取り掛かる順番の話なだけですが)

おまけ
紙を使って下書きしたときはすぐに計算をし終えたのですが、ブログに数式を書くとなると時間がかかりそうですね笑 でも書いていきます!
\begin{align}
I(s)\times\frac{(\frac{1}{Cs}+Ls)R}{(\frac{1}{Cs}+Ls)+R}&=\frac{E}{s}\\
I(s)&=\frac{(\frac{1}{Cs}+Ls)+R}{(\frac{1}{Cs}+Ls)R}\frac{E}{s}\\
&=(\frac{1}{R}+\frac{1}{\frac{1}{Cs}+Ls})\frac{E}{s}\\
&=\frac{E}{Rs}+\frac{E}{L}\frac{1}{s^2+\frac{1}{LC}}\\
&=\frac{E}{Rs}+\sqrt{\frac{C}{L}}E\frac{\frac{1}{\sqrt{LC}}}{s^2+\frac{1}{LC}}\\
&\underrightarrow{ \mathscr{L}^{-1} } \frac{E}{R}+\sqrt{\frac{C}{L}}E\mathrm{\sin}\frac{t}{\sqrt{LC}}\\
\end{align}
多分これで合ってます。
\(LC\)を流れる電流分が振動するんですね。
ラプラス変換をしてみて感じたのですが、今回は元の回路図が簡単なせいか微分方程式を解いても同じくらいの計算量になるかもしれません笑
もう少し複雑な回路にすれば、ラプラス変換の方が計算量的にも楽になってくるのが実感できましたね!失敗です。
それでは次回!

ラプラス変換をしてみて感じたのですが、今回は元の回路図が簡単なせいか微分方程式を解いても同じくらいの計算量になるかもしれません笑
もう少し複雑な回路にすれば、ラプラス変換の方が計算量的にも楽になってくるのが実感できましたね!失敗です。
それでは次回!



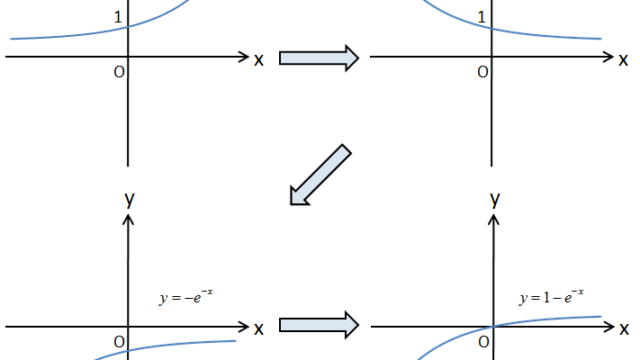









記事拝見しましたが、冒頭の画像のみ理解できました!
何かすごい!すごいぞこれは!というのが今の感想です。
二種の勉強を始めるにあたって、まずは数学だなと考え
先日、数学の参考書を注文しました。
参考書を読みつつ徐々に理解して行こうと思います!
>レベル4さん
画像につっこみありがとうございます!
ラプラスと言ったらラプ◼️スですよ!笑
今回の記事は、過渡現象を微分方程式で解ける人で、二次試験の制御をラプラス変換で解ける人ならば目から鱗の記事になってます。
かなり限定的ですし、そのレベルの人は2種合格が目前ですので、失敗した感がちょっとあります笑
確かに、電験は2種になるといきなり数学のレベルがあがりますね。
数学の参考書を買うにしても高校生向けのは範囲が膨大ですので、電験に特化した数学の参考書をお勧めします。
はじめまして、来年二種受験を考えています。
まさに「3-1.png」は目から鱗でした。
あとは式の中にω^2を作ってあげるだけ。
なんだか少し肩の荷が降りたような気がしています。
>ザッキーさん
コメントありがとうございます!
電験の参考書を読んでいると、『過渡現象は微分方程式で解くものだ!ラプラス変換は自動制御のためのツールだ!』としか言っていない気がしてなりません。過渡現象を大学の教科書から勉強するとラプラス変換を普通に使って解いているので、私も目から鱗でした笑
今からみっちり2種の勉強をすれば、来年の合格も十分可能かと思います。
頑張ってください!
はじめまして、おまけの項目の計算式で質問があります。最後から二行目の式はどのようにして式変形したのでしょうか? =E/Rs+√(C/L)*E*(1/√LC/(s^2+1/LC)の箇所です。1を√(LC/LC)に変換して√(C/L)*Eと掛けてやったのでしょうか?回答お待ちしております。
ご質問ありがとうございます。
\(\frac{1}{s^2+\frac{1}{LC}}\)に注目して、分子に\(s\)が無いことから、\(\sin\)のラプラス変換をできるように分子に\(\frac{1}{\sqrt{LC}}\)を作りに行きました。
その帳尻合わせとして(全体で式の意味が変わらないように)、\(E\)の手前に\(\sqrt{\frac{C}{L}}\)を作りました。