複雑な回路の過渡現象をラプラス変換で解く！

皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。

少し前に、ラプラス変換で過渡現象を解くと計算が捗るという記事を書きました。

ラプラス変換で解く過渡現象皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。 Twitterや2chでは合格・不合格の阿鼻叫喚となってい...

先日、ラプラス変換で解いてみると面白そうな過去問をtwitterで見つけましたので、今回はその解答例を紹介してみたいと思います。

引用問題→電験２種平成25年度一次試験理論問4

　この記事の内容

過渡現象→微分方程式という固定観念
解説の全体像
$V_{C} (t)$ の計算
- 立式する際に気にしておいてほしいこと
- 問題に戻ります
$i_{1} (t), i_{2} (t)$ の計算
$t = t_{0}$ について
コンデンサへの充電について
まとめ

過渡現象→微分方程式という固定観念

解説に入る前に、、、過渡現象は微分方程式でということが参考書の主流になっているので、その解説ももちろん微分方程式となることが殆どです。

今回の穴埋め問題は、誘導の流れに乗って微分方程式を使った方が答えやすいのかもしれませんが、問題によっては誘導文に微分方程式が出てこないことがあるので、微分方程式でもラプラス変換でもどちらを使っても構わないような時があります。それでも頑なに微分方程式で解説するのは、何故なんでしょう？

微分方程式で解く場合は立式も面倒ですし、特性方程式や指数関数を使うのも若干面倒です。一方でラプラス変換は、 $s$ 回路図を作ってしまえばオームの法則っぽく立式できますし、最後のラプラス変換公式に式変形していくのが若干面倒ではありますすが、微積分を使わない分計算が少し楽に感じます。

ケンタ

ラプラス変換は自動制御だけという固定観念も有るような気がします。

まぁ、文句はこのくらいにして、解説を作っていきましょう！

解説の全体像

問題の誘導を気持ちいいくらいに完全に無視して、先ずはラプラス変換で一気に $V_{C} (t), i_{1} (t), i_{2} (t)$ を計算してから、穴埋め問題毎に形を整えて加工していきます。

理論問題を解くときは特にそうですが、私は誘導を完全に無視して、計算した結果から適宜解答を切り出すようなことを偶にします笑　去年の電験１種二次試験でもそうしていました。誘導に乗ると窮屈に感じるときがありますので。

稀に勝手に計算しすぎて、誘導に戻ってこれなくなる時がありますが、その時はその時です。

$V_{C} (t)$ の計算

$I_{C} (s)$ が分かると、 $V_{C} (t), i_{1} (t), i_{2} (t)$ が芋づる式に分かっていきます。

先ずは、回路図を $s$ 回路図に変換してみましょう。

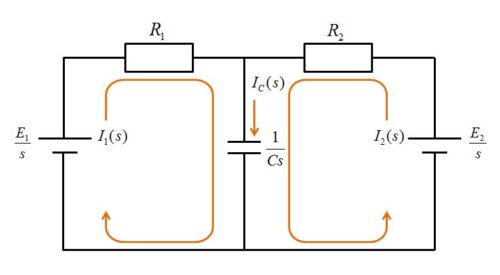
次に、条件式を立てます。

$\frac{E_{1}}{s} = R_{1} I_{1} (s) + \frac{I_{C} (s)}{C s}$ 　…式(1)

$\frac{E_{2}}{s} = R_{2} I_{2} (s) + \frac{I_{C} (s)}{C s}$ 　…式(2)

$I_{1} (s) + I_{2} (s) = I_{C} (s)$ 　…式(3)

立式する際に気にしておいてほしいこと

式を立てる上で気にしておいてほしいことに、未知数の数と式の数というのがあります。この2つの数が同じか式の数の方が多くないと、基本的に連立方程式は解けません。今回は未知数 $I_{1} (s), I_{2} (s), I_{C} (s)$ の3つに対して、式が3つあるので計算が大変かもしれませんが、解けるということは漠然と分かります。

また、闇雲に式変形をするのではなく、未知数を消去していくという目算を立ててから式変形をしていって下さい。今回で言うと

　式(1) → $I_{1} (s)$ =( $I_{C} (s)$ の式)　…式(1)’

　式(2) → $I_{2} (s)$ =( $I_{C} (s)$ の式)　…式(2)’

としてから、式(3)に代入して

　式(3) → $I_{C} (s)$ だけの式に変形できる

　　　　→ $V_{C} (t), i_{1} (t), i_{2} (t)$ が分かる

というようにです。

問題に戻ります

式(1)より　　 $I_{1} (s) = \frac{1}{R_{1}} (\frac{E_{1}}{s} - \frac{I_{C} (s)}{C s})$

式(2)より　　 $I_{2} (s) = \frac{1}{R_{2}} (\frac{E_{2}}{s} - \frac{I_{C} (s)}{C s})$

を式(3)に代入して

$\begin{array}{r} \frac{1}{R_{1}} (\frac{E_{1}}{s} - \frac{I_{C} (s)}{C s}) + \frac{1}{R_{2}} (\frac{E_{2}}{s} - \frac{I_{C} (s)}{C s}) = I_{C} (s) \end{array}$

$\frac{1}{C} (\frac{1}{R_{1}} + \frac{1}{R_{2}})$ は表記が面倒ですので、時定数 $τ$ を使って、 $1 / τ$ に置き換えます。

$\begin{aligned} \frac{1}{s} (\frac{E_{1}}{R_{1}} + \frac{E_{2}}{R_{2}}) & = I_{C} (s) (1 + \frac{1}{τ s}) \\ I_{C} (s) & = \frac{1}{1 + \frac{1}{τ s}} \frac{1}{s} (\frac{E_{1}}{R_{1}} + \frac{E_{2}}{R_{2}}) \\ V_{C} (s) & = \frac{I_{C} (s)}{C s} \\ = \frac{1}{s (s + \frac{1}{τ})} \frac{1}{C} (\frac{E_{1}}{R_{1}} + \frac{E_{2}}{R_{2}}) \\ = τ (\frac{1}{s} - \frac{1}{s + \frac{1}{τ}}) \frac{1}{C} (\frac{E_{1}}{R_{1}} + \frac{E_{2}}{R_{2}}) \\ \underset{\to}{L^{- 1}} τ (1 - e^{- \frac{t}{τ}}) \frac{1}{C} (\frac{E_{1}}{R_{1}} + \frac{E_{2}}{R_{2}}) \\ = τ \frac{1}{C} (\frac{E_{1}}{R_{1}} + \frac{E_{2}}{R_{2}}) (1 - e^{- \frac{t}{τ}}) \end{aligned}$

式変形に絶対の自信があれば、 $τ \frac{1}{C} (\frac{E_{1}}{R_{1}} + \frac{E_{2}}{R_{2}})$ を定常値 $V_{C}$ と置き替えてしまって構いませんが、念のため確認してみます。

式からは

$\begin{aligned} τ \frac{1}{C} (\frac{E_{1}}{R_{1}} + \frac{E_{2}}{R_{2}}) \\ = C \frac{R_{1} R_{2}}{R_{1} + R_{2}} \frac{1}{C} (\frac{E_{1}}{R_{1}} + \frac{E_{2}}{R_{2}}) \\ = \frac{R_{1}}{R_{1} + R_{2}} E_{1} + \frac{R_{2}}{R_{1} + R_{2}} E_{2} \end{aligned}$

一方で回路図からは、定常状態ではコンデンサに電流が流れていないので、

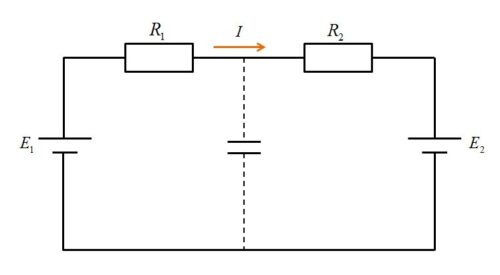
$\begin{array}{r} I = \frac{E_{1} - E_{2}}{R_{1} + R_{2}} \end{array}$

より、

$\begin{aligned} V_{C} & = E_{1} - R_{1} I \\ = \frac{R_{1}}{R_{1} + R_{2}} E_{1} + \frac{R_{2}}{R_{1} + R_{2}} E_{2} \end{aligned}$

となるので、式変形に間違いが無かったことが確認されました。

よって、

$\begin{array}{r} V_{C} (t) = V_{C} (1 - e^{- \frac{t}{τ}}) \end{array}$

より、(1)は

$\begin{array}{r} τ = \frac{1}{C} (\frac{1}{R_{1}} + \frac{1}{R_{2}}) \end{array}$

となります。

$i_{1} (t), i_{2} (t)$ の計算

$\begin{array}{r} V_{C} (s) = V_{C} (\frac{1}{s} - \frac{1}{s + \frac{1}{τ}}) \end{array}$

を式(1)’を少し変形したところに代入して、

$\begin{aligned} I_{1} (s) & = \frac{1}{R_{1}} (\frac{E_{1}}{s} + V_{C} (s)) \\ = \frac{1}{R_{1}} (\frac{E_{1}}{s} - \frac{V_{C}}{s} + \frac{V_{C}}{s + \frac{1}{τ}}) \\ = \frac{1}{R_{1}} (\frac{E_{1} - V_{C}}{s} + \frac{V_{C}}{s + \frac{1}{τ}}) \\ \underset{\to}{L^{- 1}} \frac{1}{R_{1}} [(E_{1} - V_{C}) + V_{C} e^{- \frac{t}{τ}}] \end{aligned}$

となります。

$I_{2} (s)$ についても同様に、式(2)’から

$\begin{aligned} I_{2} (s) & \underset{\to}{L^{- 1}} \frac{1}{R_{2}} [(E_{2} - V_{C}) + V_{C} e^{- \frac{t}{τ}}] \end{aligned}$

となります。

以上から(2)は

$\begin{aligned} i_{1} (0) + i_{2} (0) & = \frac{1}{R_{1}} [(E_{1} - V_{C}) + V_{C}] + \frac{1}{R_{1}} [(E_{1} - V_{C}) + V_{C}] \\ = \frac{E_{1}}{R_{1}} + \frac{E_{2}}{R_{2}} \end{aligned}$

となります。

また、(3)は

$\begin{aligned} I_{1} & = lim_{t \to \infty} i_{1} (t) \\ = \frac{E_{1} - V_{C}}{R_{1}} \\ = \frac{1}{R_{1}} (\frac{R_{1}}{R_{1} + R_{2}} E_{1} + \frac{R_{2}}{R_{1} + R_{2}} E_{2}) \\ = \frac{E_{1} - E_{2}}{R_{1} + R_{2}} \end{aligned}$

となります。

$t = t_{0}$ について

一般的に $I_{C} (t) = i_{1} (t) + i_{2} (t)$ となるので、 $I_{C} (t_{0}) = i_{1} (t_{0})$ のときは、

$\begin{aligned} I_{C} (t_{0}) & = i_{1} (t_{0}) + i_{2} (t_{0}) \\ i_{1} (t_{0}) & = i_{1} (t_{0}) + i_{2} (t_{0}) \\ i_{2} (t_{0}) & = 0 \end{aligned}$

となります。

ここから必要な条件を抽出していきます。

$\begin{aligned} i_{2} (t_{0}) & = 0 \\ \frac{1}{R_{2}} [(E_{2} - V_{C}) + V_{C} e^{- \frac{t_{0}}{τ}}] & = 0 \\ V_{C} e^{- \frac{t_{0}}{τ}} & = V_{C} - E_{2} \end{aligned}$

これを $I_{C} (t_{0})$ に代入して、(4)は

$\begin{aligned} I_{C} (t_{0}) & = i_{1} (t_{0}) + i_{2} (t_{0}) \\ = \frac{1}{R_{1}} [(E_{1} - V_{C}) + V_{C} e^{- \frac{t_{0}}{τ}}] + \frac{1}{R_{2}} [(E_{2} - V_{C}) + V_{C} e^{- \frac{t_{0}}{τ}}] \\ = \frac{1}{R_{1}} [(E_{1} - V_{C}) + (V_{C} - E_{2})] + \frac{1}{R_{2}} [(E_{2} - V_{C}) + (V_{C} - E_{2})] \\ = \frac{E_{1} - E_{2}}{R_{1}} \end{aligned}$

となります。

コンデンサへの充電について

最後です！

先ずは、コンデンサへ流れ込む $I_{C} (t)$ を求めます。

$\begin{aligned} I_{C} (t) & = i_{1} (t) + i_{2} (t) \\ = \frac{1}{R_{1}} [(E_{1} - V_{C}) + V_{C} e^{- \frac{t}{τ}}] + \frac{1}{R_{2}} [(E_{2} - V_{C}) + V_{C} e^{- \frac{t}{τ}}] \\ = (\frac{1}{R_{1}} + \frac{1}{R_{2}}) V_{C} e^{- \frac{t}{τ}} \end{aligned}$

よって(5)は

$\begin{aligned} Δ q & = \int_{t_{0}}^{\infty} I_{C} (t) d t \\ = (\frac{1}{R_{1}} + \frac{1}{R_{2}}) V_{C} [- τ e^{- \frac{t}{τ}}]_{t_{0}}^{\infty} \\ = (\frac{1}{R_{1}} + \frac{1}{R_{2}}) V_{C} e^{- \frac{t_{0}}{τ}} τ \\ = (\frac{1}{R_{1}} + \frac{1}{R_{2}}) (V_{C} - E_{2}) C \frac{1}{\frac{1}{R_{1}} + \frac{1}{R_{2}}} \\ = (V_{C} - E_{2}) C \\ = \frac{C R_{2} (E_{1} - E_{2})}{R_{1} + R_{2}} \end{aligned}$

となります。

まとめ

微分方程式を使うかラプラス変換を使うかは、好みによるところが大きいです。

ただ、理想としてはどちらも使えるようにしておいたほうが良いです。今回のように微分方程式を前提とした誘導文だと、微分方程式を使って解いていったほうが省エネっぽそうですし。

手札は数が多い事に越したことはありませんからね。

それでは次回！

【2022.9.16更新】「電験２種過渡現象をラプラス変換で解く27年間 2021度版」は好評発売中です！

「電験２種過渡現象をラプラス変換で解く30年間 2025年版」のご紹介電験２種一次試験の過渡現象を煩雑な微分方程式ではなく、簡易なラプラス変換で解説しています。本書を理解することで、電験２種二次試験の自動制御だけではなく、電験１種一次試験の過渡現象にも対応できるようになります。...

理論過渡現象微分方程式ラプラス変換 s回路

複雑な回路の過渡現象をラプラス変換で解く！

過渡現象→微分方程式という固定観念

解説の全体像

$V_{C} (t)$ の計算

立式する際に気にしておいてほしいこと

問題に戻ります

$i_{1} (t), i_{2} (t)$ の計算

$t = t_{0}$ について

コンデンサへの充電について

まとめ

【参考になるのか？】私の勉強方法

加法定理さえ覚えておけば半角・倍角・3倍角の公式を覚える必要がない

部分積分って何だ？

オペアンプをまとめて覚える方法

計算問題を素早く解くには？

パワーエレクトロニクスの対策～自己流編その１～

【参考になるのか？】私の勉強方法

加法定理さえ覚えておけば半角・倍角・3倍角の公式を覚える必要がない

部分積分って何だ？

オペアンプをまとめて覚える方法

計算問題を素早く解くには？

パワーエレクトロニクスの対策～自己流編その１～

COMMENT コメントをキャンセル

電験２種二次試験の攻略方法

進相コンデンサは無効電力を消費するし供給もする？！

オペアンプをまとめて覚える方法

過渡現象→微分方程式という固定観念

解説の全体像

VC(t)の計算

立式する際に気にしておいてほしいこと

問題に戻ります

i1(t),i2(t)の計算

t=t0について

コンデンサへの充電について

まとめ

【参考になるのか？】私の勉強方法

加法定理さえ覚えておけば半角・倍角・3倍角の公式を覚える必要がない

部分積分って何だ？

オペアンプをまとめて覚える方法

計算問題を素早く解くには？

パワーエレクトロニクスの対策 ～自己流編その１～

【参考になるのか？】私の勉強方法

加法定理さえ覚えておけば半角・倍角・3倍角の公式を覚える必要がない

部分積分って何だ？

オペアンプをまとめて覚える方法

計算問題を素早く解くには？

パワーエレクトロニクスの対策 ～自己流編その１～

COMMENT コメントをキャンセル

電験２種二次試験の攻略方法

進相コンデンサは無効電力を消費するし供給もする？！

オペアンプをまとめて覚える方法

$V_{C} (t)$ の計算

$i_{1} (t), i_{2} (t)$ の計算

$t = t_{0}$ について

パワーエレクトロニクスの対策～自己流編その１～

パワーエレクトロニクスの対策～自己流編その１～