過渡現象にラプラス変換を適応できる理由

皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。

当ブログでは「ラプラス変換を使って過渡現象を解ける」ということを何度か主張しています。

ラプラス変換で解く過渡現象皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。 Twitterや2chでは合格・不合格の阿鼻叫喚となってい...

複雑な回路の過渡現象をラプラス変換で解く！皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。 少し前に、ラプラス変換で過渡現象を解くと計算が捗るという記...

その肝心の具体的な理由については、きちんと説明してくるのをなかなかしてこなかったわけですが、今回きちんと説明してみます。

そもそも「ラプラス変換」とは？

きちんと説明するには、ラプラス変換の原則に則った説明をする必要があります。

時間$t$の関数である$f(t)$をラプラス変換して、$F(s)$という関数を得ようとしたときには、

$$\begin{array}{r}{\displaystyle {\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-st}f(t)\mathrm{d}t}\end{array}$$

という計算をする必要があります。

ここで$s$はラプラス演算子と呼ばれ、数学的演算をするための単純なツールのようなものです。$\mathit{s}$が表現する特定の物理量があるわけではありません。この演算子を使ってラプラス変換をすると、普通であれば微分方程式を解くところを省エネして四則演算で解けるようになるというだけです。

逆ラプラス変換をするのに別途いくつか覚える公式（下表のようなラプラス変換表の公式です）がありますが、二次試験の機械・制御でどちらにせよ覚えなければいけなくなります。

ケンタ

電験で使用頻度の高い公式はこれくらいです。

微分方程式をラプラス変換してみる

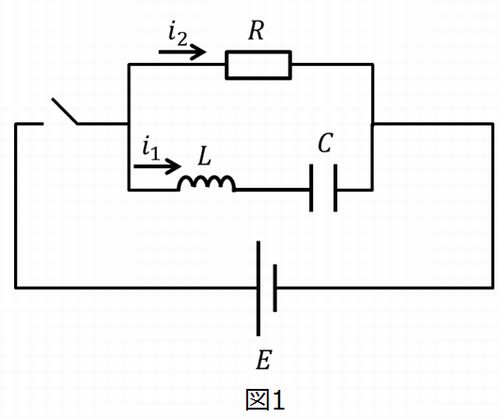
図1から式(1)(2)の微分方程式を立てることができます。

$$\begin{array}{rl}L\frac{\mathrm{d}{i}_1}{\mathrm{d}t}+\frac{1}{C}{\displaystyle {\int }_0^t{i}_1\mathrm{d}t}& =E\dots (1)\\ R{i}_2& =E\dots (2)\end{array}$$

この式(1)(2)全体について、ラプラス変換をしていきます。

式(1)のラプラス変換

式(1)をラプラス変換すると

$$\begin{array}{r}Ls{I}_1(s)+\frac{I_1(s)}{Cs}=\frac{E}{s}\dots (1{)}^{\prime }\end{array}$$

となります。

【番外編】過渡現象にラプラス変換を適応できる理由皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。 以前の記事で計算を省略していたところを、少し丁寧に解説して...

微分・積分演算子をラプラス変換する厳密なところを理解するようとすると、結構面倒ですが、

$$\begin{array}{r}Ls⟷\omega L,\frac{1}{Cs}⟷\frac{1}{\omega C}\end{array}$$

と交流回路のインピーダンスと対応して覚えると楽です。

また、$i_1(t)$をラプラス変換したものが$I_1(s)$です。ラプラス変換の式できちんと表すと、

$$\begin{array}{r}{I}_1(s)={\displaystyle {\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-st}{i}_1(t)\mathrm{d}t}\end{array}$$

となります。

ケンタ

余談ですが、ラプラス変換の定義式は二次試験の過去問で出題されたことがあります。

同じく、$E$をラプラス変換したものが$\frac{E}{s}$となります。こちらも、ラプラス変換の式できちんと表すと、

$$\begin{array}{r}{\displaystyle {\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-st}E\mathrm{d}t=\frac{E}{s}}\end{array}$$

となりますが、定数$E$をラプラス変換すると単純に分母に$s$がくるだけです。これは二次試験で覚えるラプラス変換表に入ってきます。

ケンタ

腕試しとして、↑の積分をきちんとできるかやってみると面白いかもしれません。

式(2)のラプラス変換

式(2)についても同様にラプラス変換をしてみると

$$\begin{array}{r}R{I}_1(s)=\frac{E}{s}\dots (2{)}^{\prime }\end{array}$$

となります。

式(1)'(2)’が表しているオームの法則的なものを逆算して回路図に落とし込むと、図2の$s$回路図になります。

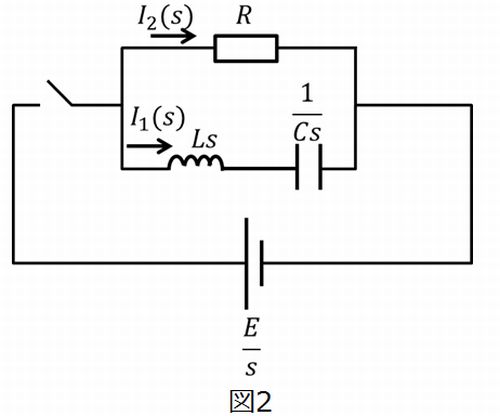
このように、ラプラス変換した文字式を、それぞれ電圧、電流、抵抗などの素子に近い形に置き換えて作図することができます。

$t$回路図と$s$回路図の行き来

この記事で説明してきたことを図3のフローで再度説明すると、①→②→⑤→④をしたことになります。

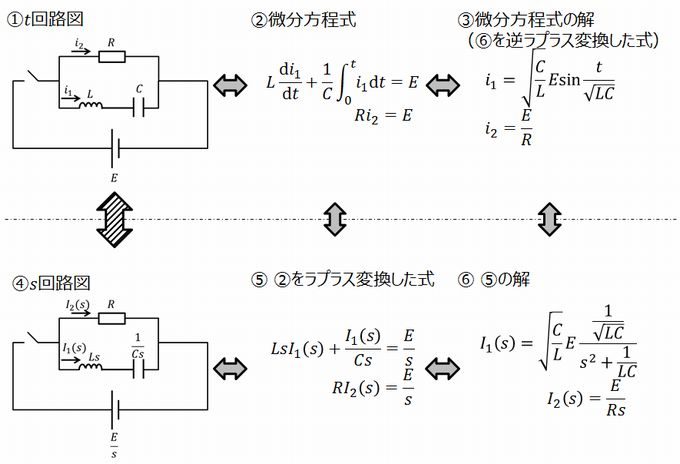
これらの操作は等価的に行ったり来たりすることができる数学的な操作ですので、一定の約束事を作れば、 ④の回路図を①から直接作ってしまっても問題がありません。「ラプラス変換で解く過渡現象」ではそれを利用して、①→④→⑤→⑥→③ということをしています。

ケンタ

「一定の約束事」とは、$s$を使って交流回路的に$s$回路図をかくことです。

①→④→⑤→⑥→③という順番を辿るメリット

①→④→⑤→⑥→③という順番を辿るメリットは大きく2つあります。

メリット1つは、回路図をかいて式を立てるという、直流回路や交流回路で何度もしてきたことに置き換えられるということです。

もう1つは、逆ラプラス変換の公式を覚えておけば、ラプラス変換の定義通りに微積分の演算子を変換する必要がないからです。

このように、ラプラス変換を利用することで、省エネをして過渡現象の問題を解くことができるようになります。

まとめ

今回は、「過渡現象を解くのになぜラプラス変換を使えるのか?」というところを、数学の根本的なところに立ち返って説明してみました。

ラプラス変換や過渡現象、微分方程式は数学的に説明しやすいところで、電気科卒でないけど理系のバックグラウンドがある人は取り掛かりやすい単元かと思います。

「こういったこともできるんだなぁ」と少しでも感じてもらえれば幸いです！

それでは次回！