同期機の位相調節はまとめて覚えられる

皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。

いつも理論科目の記事が目立つ独自解釈シリーズですが、今回は趣向を変えて機械科目の内容を書いてみようかと思います。

毎回数学チックな話に持っていきがちですが、すみません、今回もそうなります笑

ケンタ

独自解釈シリーズは、あまり電気のことは詳しくない私が、主に数学的にどうこじつけて電験の問題に対処していったかの記事となります。

この記事の到達目標

機械科目って理論科目と同じくらい計算ばっかりで、回路図の登場が多いですよね。同期機とか誘導機とか変圧器とか。今回のテクニックを使えるようになると、

の界磁電流の強弱と位相調節の向きについて、似たようなベクトル図を使っで解けるようになります。それでは1つずつ説明していきます。

同期電動機のV曲線

同期電動機は外部から電源を繋げて初めて動きますので、当たり前ですが負荷となります。

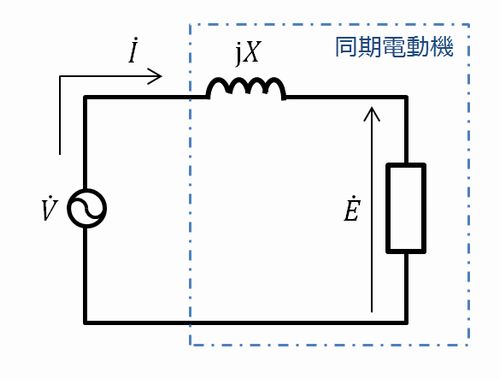
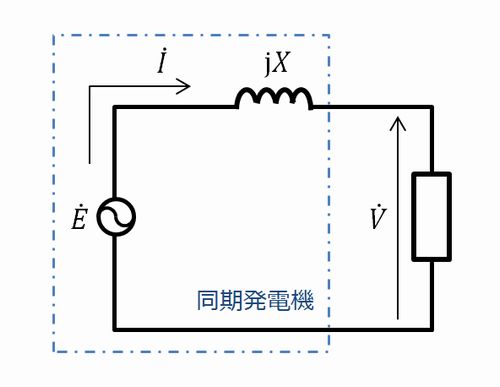
この回路図から式を立てると、

\begin{align}\dot{V}=\dot{E}+\mathrm{j}X\dot{I}\\ \end{align}

となります。ということで、ベクトル図にすると以下の通りに表せます。

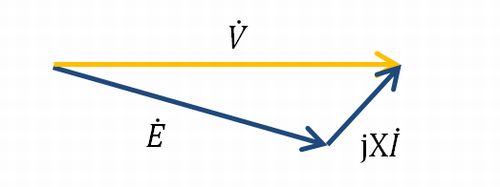
このベクトル図が本日の内容の肝となります。

【詳しく！】ベクトル図の書き方について

いきなり↑のベクトル図を書いてしまいましたが、もう少し丁寧に1つ1つ説明してみます。この説明を理解しておけないと、最後の位相のところで「？？」となってしまうからです。

先ず、負荷電流が電源電圧より遅れているとします。

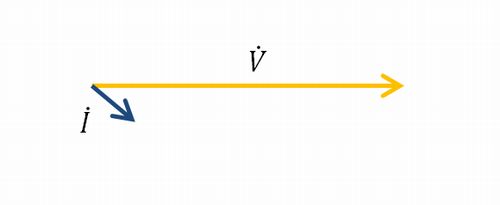
これに対して、\(X\dot{I}\)と言うのは負荷電流(\(\dot{I}\))の実数倍(\(X\)倍)ということです。つまり、\(\dot{I}\)のベクトルの向きを変えずに延長させたということです。

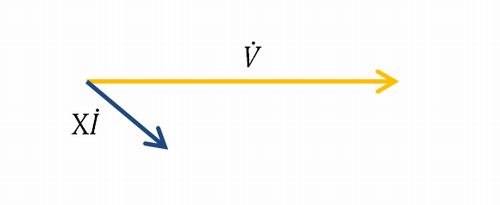
この\(X\dot{I}\)に\(\mathrm{j}\)が付くのは、\(X\dot{I}\)を反時計方向に\(90^{ \circ }\)回転することを意味します。なぜ回転を意味するのかをきちんと証明しようとすると面倒ですが、簡単に説明すると、\(1+\mathrm{j}0\)という複素数に\(\mathrm{j}\)を掛けると\(0+\mathrm{j}\)となり、反時計方向に\(90^{ \circ }\)させたことになるからです。

ということで↓の様な図となり、

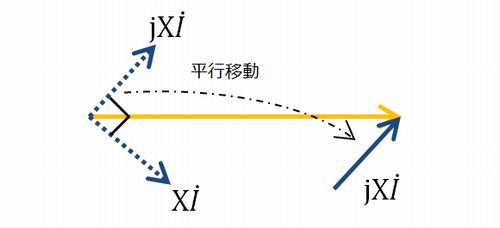
\(\dot{V}\)と\(\mathrm{j}X\dot{I}\)のギャップを埋めるように、\(\dot{E}\)が入ってきます。

本題に戻ります

同期電動機の回転部分には電磁石がありますので、その界磁電流を強めるということは、内部誘導起電力\(\boldsymbol{\dot{E}}\)が大きくなるということです。

ということは、先程のベクトル図が↓のように若干変形します。

ケンタ

本当は\(\dot{V}\)と\(\dot{E}\)からなる相差角（\(\angle \delta\)で表現したりします）も変わったりしますが、話を簡単にするために無視します。
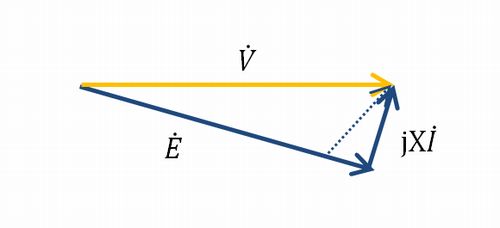
詳しく把握したい方は、下の方のコメント欄をご参照下さい。

何となく分かってきましたか？この\(\mathrm{j}X\dot{I}\)の角度のズレが、元をたどると\(\dot{I}\)が反時計回りに回転するになり、引いては位相が進むことになります。

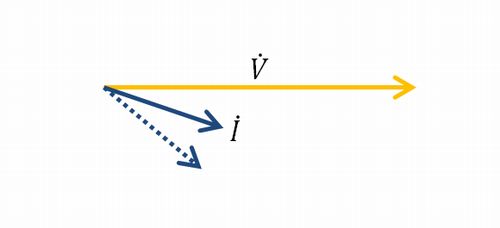
ということで、同期電動機は界磁電流を強めると負荷電流の位相が進みます。

同期発電機の進相運転

次は同期発電機の進相運転についてです。

同期発電機を適当な負荷に接続して、負荷内部の電圧降下は無視して、負荷端の電圧を\(\dot{V}\)とします。

諸々の説明を省略して、ここから以下のベクトル図を作ります。

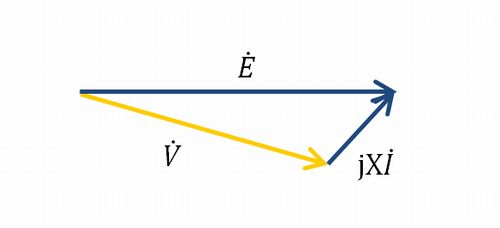
同期発電機の界磁電流を弱めると、内部誘導起電力\(\boldsymbol{\dot{E}}\)が小さくなるということです。ということは↓のように変形して、

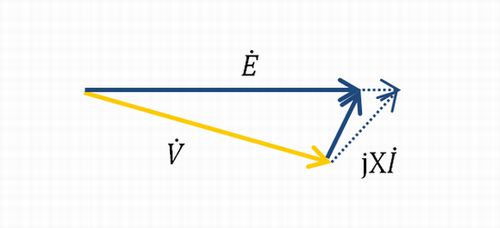
\(\dot{I}\)に注目すると、

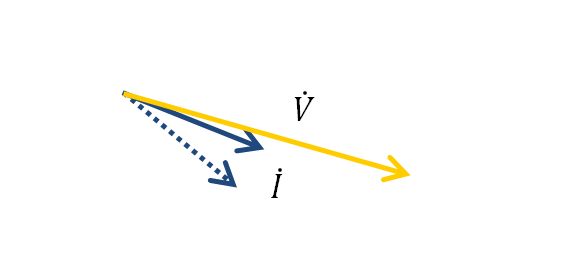
負荷電流の位相が進んだことが分かります。

ということで、同期発電機は界磁電流を弱めると負荷電流の位相が進みます。

ケンタ

説明を分かりやすくするために同期発電機の場合は、界磁電流を弱める方で説明をしました。「取り敢えず界磁電流を強めてみたら負荷電流の位相が遅れたから、進相運転はその逆か！」という判断でも良いと思います。というか、私は同期電動機・同期発電機に関わらず、いつも取り敢えず強める方向でベクトル図を書いています笑

まとめ

電験では様々なところに今回取り上げたようなベクトル図が出てきます。これが書けるようになってくると、単純暗記が少なくなってきたり、公式を忘れた時の導出ができるようになったりします。

例えば、同期発電機の出力

\begin{align}P=\frac{V_\mathrm{c}\dot{V’}}{X}\sin\delta\\ \end{align}

なんかもベクトル図を使った導出をしています。

↑の導出は必ず参考書に載っていますので、ベクトル図を使って勝手に解釈をしていた、参考書に載っていないようなテクニックを他にも見つけましたら、また紹介します。

それでは次回！