電験に必要な微積分学とは

皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。

電験は数学と切っても切れない関係にあります。

３種から早くも複素数を扱い始め、２種からはついに微積分を扱い始めます。

ケンタ

１種では行列が登場してきますが、それはまたの機会に

電験での微積分の問題は、物理現象を数式で立式して計算してく問題が多く、微小区間の考え方ができていると比較的楽に解けることがあります。

その典型的な例は電験２種理論のガウスの法則であったりしますが、殆どが理論科目に集中しているが故に、電験２種一次試験では理論が鬼門という人が多いかと思います。

ブログで書けることには限りがありますが、基礎的な考え方を紹介することで皆さんの理解の一助になれば幸いです。

電験で微積分が登場する単元とは？

電験３種

あまりないですが、強いてあげるのならばレンツの法則です。

$$\begin{array}{rl}V& =-N\frac{\mathrm{d}\Phi }{\mathrm{d}t}\end{array}$$

という式です。

微分は変化速度を表しますので、「磁束の変化を妨げるように電圧が発生する」という現象から立式することができます。式をそのまま覚えてもいいのですが、コイルに磁石を近づけると電圧が発生するという現象だけをイメージで持っておくと、その場で立式することができるようになります。

電験２種

ざっと挙げますと、主に以下になります。

「微小区間→積分」と書いてある単元は、微小区間の立式（下の方で説明します）をしてから、それを拡張、つまり積分して計算する単元です。

理論

1. ガウスの法則（微小区間→積分）
2. 非柱状抵抗（微小区間→積分）
3. 過渡現象（微分方程式）
4. ビオ・サバールの法則（微小区間→積分）
5. アンペールの周回積分（実際に線路積分をすることは無いですが、微小区間→積分）

電力

1. 配電路の電力ロス（微小区間→積分）

機械

1. 制御、ラプラス変換（積分、微分方程式）
2. 変圧器の温度上昇試験（微分方程式）

エネルギー管理士（おまけ）

エネルギー管理士試験でも微積分が必要になる問題があります。

1. 運動方程式（微分⇔積分の行き来）
2. 回転方程式（運動方程式との対応）

上記の（　）内の説明も下の方でします。

電験に必要な微積分のエッセンス

最初にも書いているように、電験２種では微小区間の考え方が出来ているかが重要になってきます。この計算をする際に当たり前のように積分や微分の公式が出てきますが、こちらはもう覚えるしかありません。

微分方程式などで出てくる

$$\begin{array}{rl}{\displaystyle \int \frac{\mathrm{d}x}{x}}& ={\log }_{\mathrm{e}}x+C\end{array}$$

などです。

微小区間の考え方

以前のパワエレの記事で以下のような説明をしました。

ケンタ

ちなみに積分とは、微小面積$\sqrt{2}E\sin \theta \times \mathrm{d}\theta$（$\mathrm{d}$は微小の意味）を積分区間にわたって、足していくようなものです。${\displaystyle \sum \sqrt{2}E\sin \theta \mathrm{d}\theta }$と書いた方がイメージしやすいかもしれません。

概念図を使ってもう少し詳しく説明していきます。

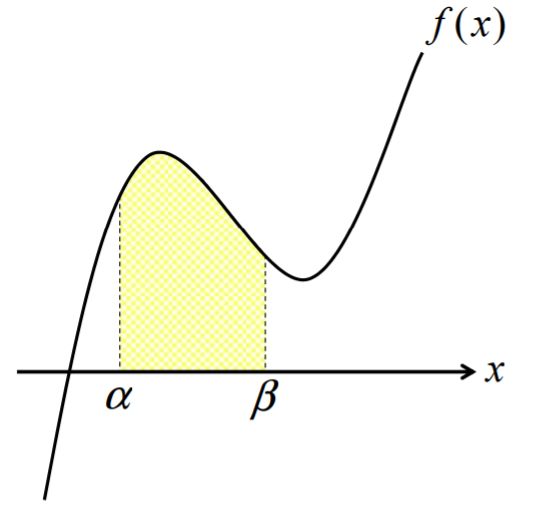
よく見る公式

$$\begin{array}{rl}{\displaystyle {\int }_{\alpha }^{\beta }f(x)\mathrm{d}x}& =F(\alpha )-F(\beta )\end{array}$$

の値はグラフで言うと以下の黄色の面積に相当します。

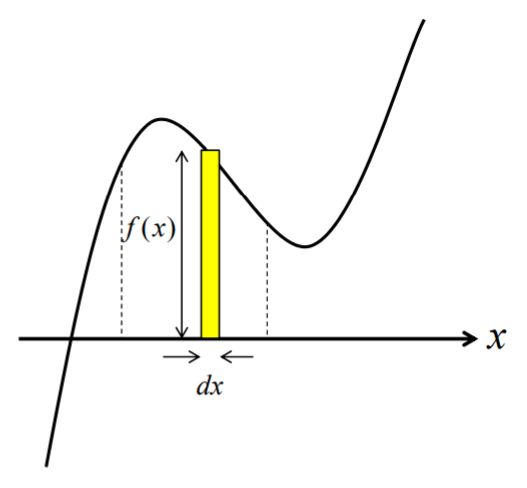
この公式の中にある$f(x)\mathrm{d}x$とは微小面積を表していて、次の図にある細長い長方形に相当します。

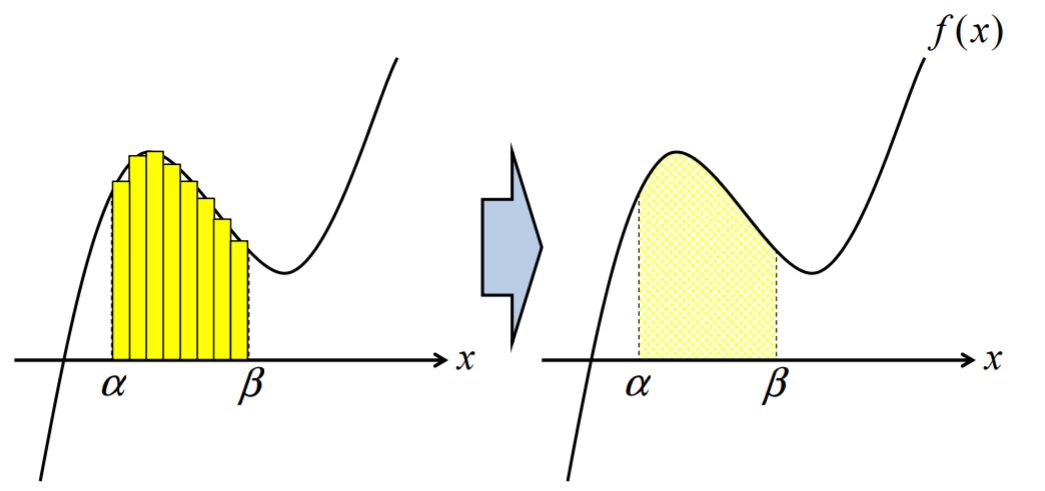
この微小面積を積分区間に渡って足していく、つまり${\displaystyle {\int }_{\alpha }^{\beta }}$していくことになります。

この考え方は3次元にも応用することができ、球の体積を求めるときにも使えます。球を輪切りにした断面で説明していきます。

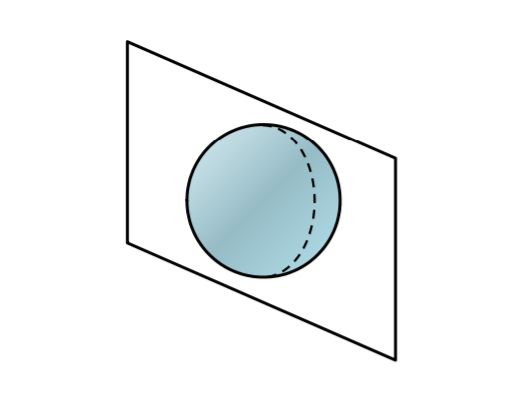
球の中心から$r$離れたところにある、微小体積$\mathrm{d}V$は表面積$4\pi r^2$を使って$\mathrm{表}\mathrm{面}\mathrm{積}\times \mathrm{d}r$と表せます。これを$0$から球の半径$a$まで積分していくと球の体積を求めることができます。「玉ねぎ」みたいな計算をしています。

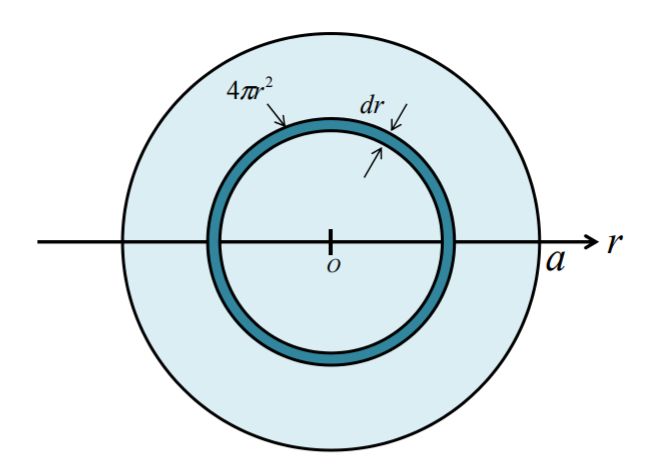
つまり

$$\begin{array}{rl}\mathrm{d}V& =4\pi r^2\mathrm{d}r\\ {\displaystyle {\int }_0^a\mathrm{d}V}& ={\displaystyle {\int }_0^{a}4\pi r^2\mathrm{d}r}\\ V& =\frac{4}{3}\pi a^3\end{array}$$

となります。

また、逆に球の体積$V$を微分すると表面積を求めることができます。

$$\begin{array}{rl}\frac{\mathrm{d}V}{\mathrm{d}r}& =\frac{\mathrm{d}}{\mathrm{d}r}\left(\frac{4}{3}\pi r^3\right)\\ & =4\pi r^2\end{array}$$

微分⇔積分　の行き来

エネルギー管理士では速度や加速度の問題が頻繁に出題されます。

そこにも微積分の考え方があり、微積分を使うと各公式を覚えなくてすみます。

先ず、加速度・速度・距離は時間$t$をパラメータとした微分⇔積分の関係にあります。これは単位から見ても感覚的に分かるかと思います。

$$\begin{array}{rl}a& =\frac{\mathrm{d}v}{\mathrm{d}t}\end{array}$$

ですので、単位だけの式で見ると

$$\begin{array}{rl}\frac{m}{s^2}& =\frac{1}{s}\times \frac{m}{s}\end{array}$$

となります。

ケンタ

$\frac{\mathrm{d}}{\mathrm{d}t}$の$\mathrm{d}$とは「微小な」という意味ですので無次元となります。定数と同じということですね。

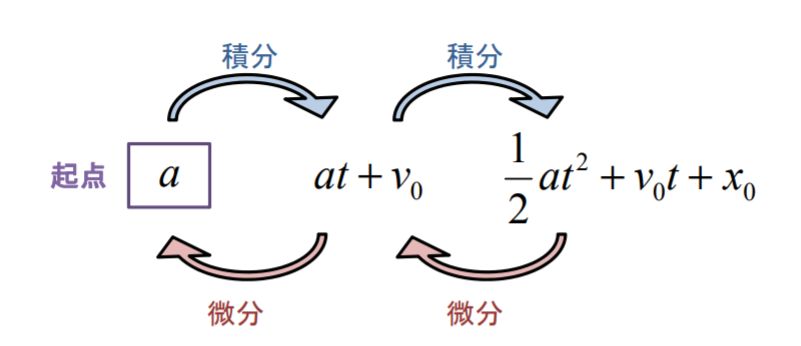
そこで、加速度$a$（定数）を起点として、$t$で積分をしていくと距離の公式を導出することができます。

【電験２種】管理人がお勧めする数学の参考書皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。 6月に入り試験がだんだん間近に迫ってきましたね。 この時...

回転方程式（おまけ）

運動方程式

$$\begin{array}{rl}m\frac{\mathrm{d}v}{\mathrm{d}t}& =F\end{array}$$

を覚えている方は、

置き換えることで、回転方程式

$$\begin{array}{rl}J\frac{\mathrm{d}\omega }{\mathrm{d}t}& =T\end{array}$$

を作ることができます。

そもそも回転方程式とは、剛体の回転を表す方程式となります。ですので、運動方程式で使用していたパラメータを回転時のパラメータに置き換えると、うまく回転方程式をか必要があります。

ケンタ

「剛体」の対義語に「質点」があります。質点とは質量のある点のことで、大きさがありません。ですので、質点を扱うときは運動方程式で運動を考えるだけで、回転を考えなくて済みます。対して剛体とは変形することのない大きさ・質量のある物体ということですので、運動と回転の両方を考える必要があります。

回転における力のようなパラメータはトルクに対応します。トルクの単位はN・mで、同じ力でも作用点との距離が遠くなるほど大きくなり、「てこ」を上手に表現した物理量になります。回転のイメージとも合うのではないでしょうか。

また、回転における速度は角速度に相当します。これは違和感が少ないかと思います。

最後に、慣性モーメントについて。重いものが小さな力だと動きにくいように、慣性モーメントが大きいと、回転がしにくくなります。これは公式からもわかります。$T$が一定のとき、$J$が大きくなると角加速度（公式で言う$\frac{\mathrm{d}\omega }{\mathrm{d}t}$です。）が小さくなります。つまり、角速度の加速が悪くなります。

まとめ

高校では数学で微積分を教え、物理では微積分を使わずに現象を説明しています。

対して電験では、現象を微積分で表せるようになっておくと色んな手間が省けます。

今回はその一例を紹介してみましたが、いかがでしたでしょうか。

もう少し噛み砕いた説明ができればよかったのですが、結構限界に近かったです笑

それでは次回！

パワーエレクトロニクスの対策～チョッパ編～皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。 遂に試験まであと１週間ですね。 土曜に電験１・２種一次試...

パワーエレクトロニクスの対策～自己流編 完結編～皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。 試験前の白熱期のせいか、当ブログのPV数が急上昇しています...