皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
遂に試験まであと1週間ですね。
土曜に電験1・2種一次試験を受けた後に、日曜に電験3種を受ける方は特に体調管理に気をつけてください!
あと、試験会場までの公共交通機関は使い慣れていない人が殆どかと思いますので、余裕を持った行動を! バスを使う場合、Google mapではバス停の位置表示が適当なので、きちんとバス会社のバス停マップを確認しておくことをお勧めします。見つからないと本当に焦りますよ笑(←経験者)
さて、今回はペンディングしていましたパワエレの続きです。

今回はチョッパについて書いていきます。
そもそもチョッパとは?

私は電気科卒ではないので、パワーエレクトロニクス全般に関する知識が浅いです。電験の範囲でしか知識がありません。
そうした私が最初にパワエレの勉強をし始めたとき、「チョッパ」という言葉に馴染みがありませんでした。(某海賊漫画を除いて笑)
チョッパには以下の意味があります。
chopper:【名詞】(なた・おのなどで)ぶち切る人
DC/DCコンバータの電圧動作に見られるような「電圧のぶつ切り」が名称の由来のように感じました。実際調べてみたところ、そのような意味合いだそうですね。
電験には
- 降圧チョッパ
- 昇圧チョッパ
- 昇降圧チョッパ
の3種類がそれぞれの電圧公式とともに登場してきます。が、私は違いを把握していません。と言いますのも、僅かな公式の違いを含めて覚えるのが無理と感じたので、回路図から電圧の公式を導出できるようにしておき、その公式から降圧なのか、昇圧なのか、昇降圧なのかを判断しておけるようにしておいたからです。
ということで、それぞれの公式を導出する方法を今回は紹介します。
降圧チョッパ
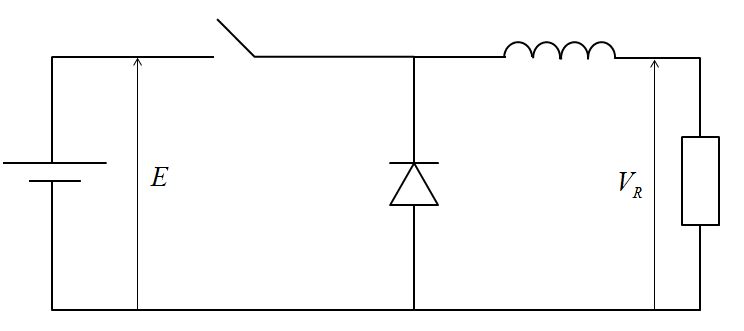
このような図が問題で与えられたとします。
スチッチがONのとき
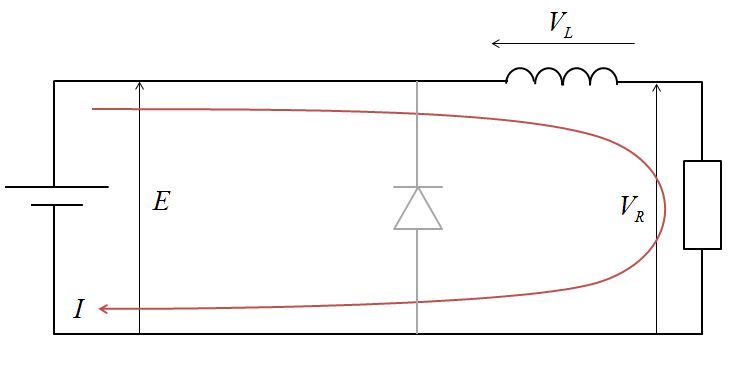
この回路のスチッチがONのときは、電源はコイルと抵抗に電力を供給します。
時間\(T_{\mathrm{ON}}\)の間にコイルに蓄えられるエネルギー\(K_{\mathrm{ON}}\)は
\begin{align}
K_{\mathrm{ON}}&=V_{\mathrm{L}}IT_{\mathrm{ON}}\\
&=(E-V_{\mathrm{R}})IT_{\mathrm{ON}}\\
\end{align}
となります。
この式となった理由を原則に基づいて説明します。
エネルギー(電力量)の定義は
\begin{align}\displaystyle \int V(t)I(t) \mathrm{d}t\\ \end{align}
であり、今回\(V(t)\)に相当する\(V_{\mathrm{L}}\)は一定電圧の\(E\)と\(V_{\mathrm{R}}\)の差で表されるので、定数となって\(\displaystyle \int\)の外に出てきます。
同様に\(I(t)\)に相当する\(I\)も一定電流ですので、\(\displaystyle \int\)の外に出てきます。
\begin{align}
K_{\mathrm{ON}}&=\displaystyle \int_{0}^{T_{\mathrm{ON}}}V_{\mathrm{L}}I\mathrm{d}t\\
&= V_{\mathrm{L}}I\displaystyle \int_{0}^{T_{\mathrm{ON}}} \mathrm{d}t\\
&=V_{\mathrm{L}}IT_{\mathrm{ON}}\\
&=(E-V_{\mathrm{R}})IT_{\mathrm{ON}}\\
\end{align}
スチッチがOFFのとき
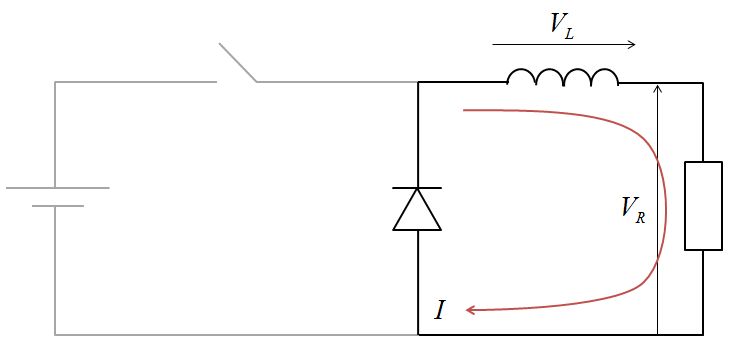
コイルが放出するエネルギー\(K_{\mathrm{OFF}}\)は
\begin{align}
K_{\mathrm{OFF}}&=V_{\mathrm{L}}IT_{\mathrm{OFF}}\\
&=V_{\mathrm{R}}IT_{\mathrm{OFF}}\\
\end{align}
となります。
1周期で
1周期\(T(=T_{\mathrm{ON}}+T_{\mathrm{OFF}})\)で考えると、コイルに蓄えられるエネルギー\(K_{\mathrm{ON}}\)とコイルから放出されるエネルギー\(K_{\mathrm{OFF}}\)が一致します。
つまり、
\begin{align}
K_{\mathrm{ON}}&=K_{\mathrm{OFF}}\\
(E-V_{\mathrm{R}})IT_{\mathrm{ON}}&=V_{\mathrm{R}}IT_{\mathrm{OFF}}\\
ET_{\mathrm{ON}}&=V_{\mathrm{R}}(T_{\mathrm{ON}}+T_{\mathrm{OFF}})\\
V_{\mathrm{R}}&=\frac{T_{\mathrm{ON}}}{T_{\mathrm{ON}}+T_{\mathrm{OFF}}}E\\
&=\frac{T_{\mathrm{ON}}}{T}E\\
\end{align}
となります。
\(0 \leqq \frac{T_{\mathrm{ON}}}{T} \leqq 1\)ですので、この公式から「降圧チョッパ」だと分かります。
昇圧チョッパ
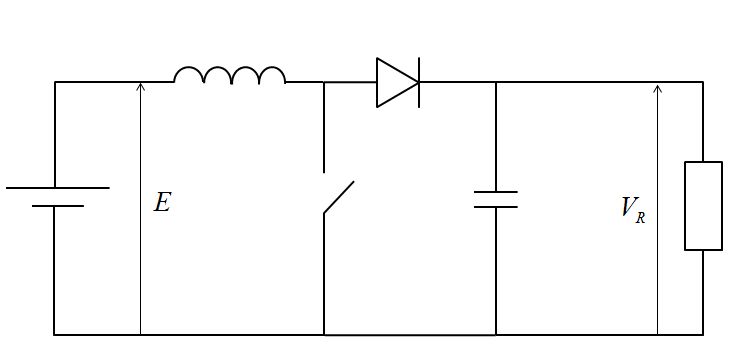
このような図が問題で与えられたとします。
スチッチがONのとき
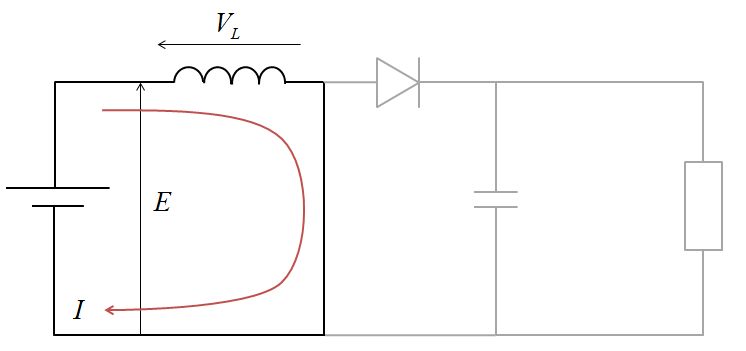
この回路のスチッチがONのときは、電源はコイルに電力を供給します。
時間\(T_{\mathrm{ON}}\)の間にコイルに蓄えられるエネルギー\(K_{\mathrm{ON}}\)は
\begin{align}
K_{\mathrm{ON}}=EIT_{\mathrm{ON}}\\
\end{align}
となります。
スチッチがOFFのとき
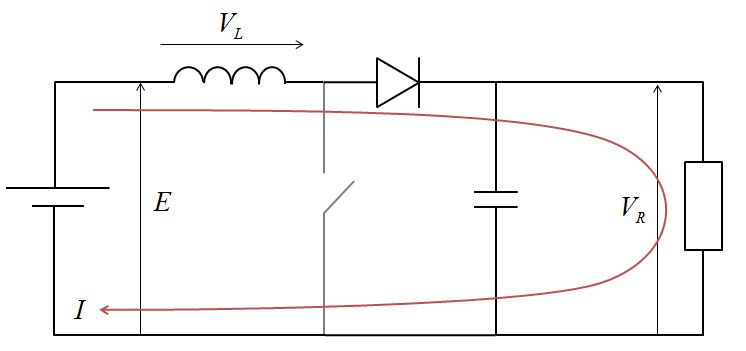
コイルは蓄えたエネルギーを放出するので、電圧の方向が電源と同じとなります。つまり、 \begin{align}
V_{\mathrm{R}}&=E+V_{\mathrm{L}}\\
\end{align}
となります。
よって、コイルが放出するエネルギー\(K_{\mathrm{OFF}}\)は
\begin{align}
K_{\mathrm{OFF}}&=V_{\mathrm{L}}IT_{\mathrm{OFF}}\\
&=(V_{\mathrm{R}}-E)IT_{\mathrm{OFF}}\\
\end{align}
となります。
1周期で
1周期\(T(=T_{\mathrm{ON}}+T_{\mathrm{OFF}})\)で考えると、コイルに蓄えられるエネルギー\(K_{\mathrm{ON}}\)とコイルから放出されるエネルギー\(K_{\mathrm{OFF}}\)が一致します。
つまり、
\begin{align}
K_{\mathrm{ON}}&=K_{\mathrm{OFF}}\\
EIT_{\mathrm{ON}}&=(V_{\mathrm{R}}-E)IT_{\mathrm{OFF}}\\
E(T_{\mathrm{ON}}+T_{\mathrm{OFF}})&=V_{\mathrm{R}}T_{\mathrm{OFF}}\\
V_{\mathrm{R}}&=\frac{T_{\mathrm{ON}}+T_{\mathrm{OFF}}}{T_{\mathrm{OFF}}}E\\
&=\frac{T}{T_{\mathrm{OFF}}}E\\
\end{align}
となります。
\(1 \leqq \frac{T}{T_{\mathrm{OFF}}}\)ですので、この公式から「昇圧チョッパ」だと分かります。
昇降圧チョッパ
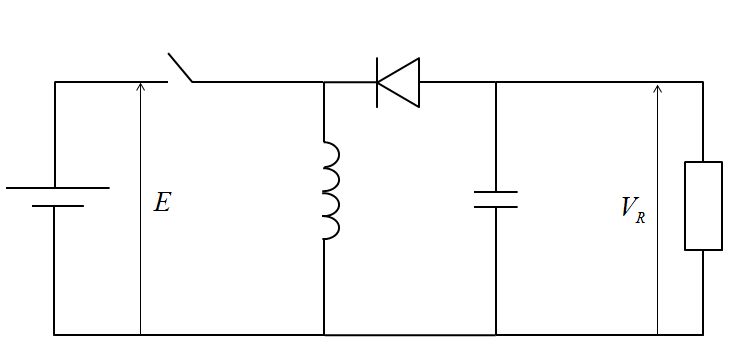
このような図が問題で与えられたとします。
スチッチがONのとき
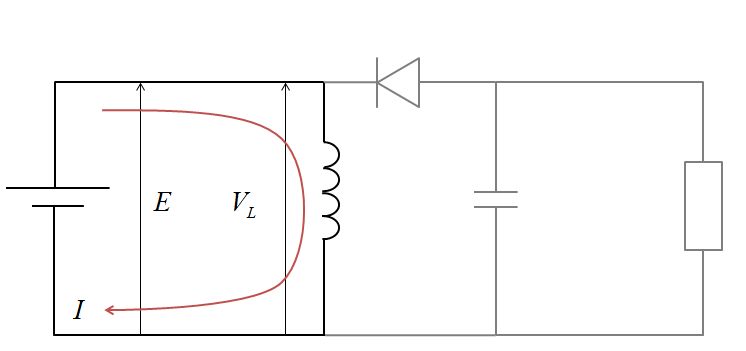
昇圧チョッパのときと同様に、時間\(T_{\mathrm{ON}}\)の間にコイルに蓄えられるエネルギー\(K_{\mathrm{ON}}\)は
\begin{align}
K_{\mathrm{ON}}=EIT_{\mathrm{ON}}\\
\end{align}
となります。
スチッチがOFFのとき
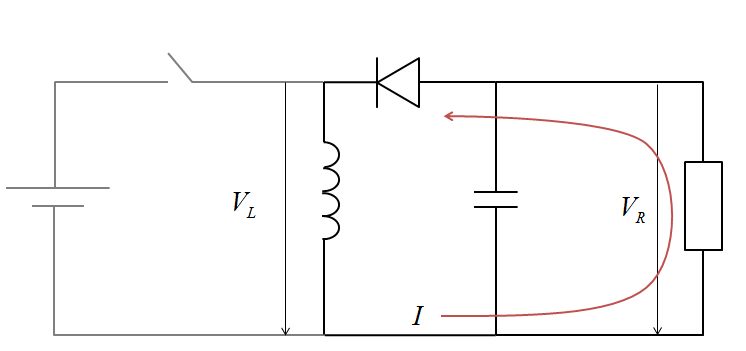
コイルが放出するエネルギー\(K_{\mathrm{OFF}}\)は
\begin{align}
K_{\mathrm{OFF}}&=V_{\mathrm{L}}IT_{\mathrm{OFF}}\\
&=V_{\mathrm{R}}IT_{\mathrm{OFF}}\\
\end{align}
となります。
1周期で
1周期\(T(=T_{\mathrm{ON}}+T_{\mathrm{OFF}})\)で考えると、コイルに蓄えられるエネルギー\(K_{\mathrm{ON}}\)とコイルから放出されるエネルギー\(K_{\mathrm{OFF}}\)が一致します。
つまり、
\begin{align}
K_{\mathrm{ON}}&=K_{\mathrm{OFF}}\\
EIT_{\mathrm{ON}}&=V_{\mathrm{R}}IT_{\mathrm{OFF}}\\
V_{\mathrm{R}}&=\frac{T_{\mathrm{ON}}}{T_{\mathrm{OFF}}}E\\
\end{align}
となります。
\(T_{\mathrm{ON}} \geqq T_{\mathrm{OFF}}\)、つまりスイッチをONにしている時間の方が長いときは、\(1 \leqq \frac{T_{\mathrm{ON}}}{T_{\mathrm{OFF}}}\)ですので昇圧となります。
逆に、\(T_{\mathrm{ON}} \lt T_{\mathrm{OFF}}\)、つまりスイッチをOFFにしている時間の方が長いときは、\(0 \lt \frac{T_{\mathrm{ON}}}{T_{\mathrm{OFF}}} \lt 1\)ですので降圧となります。
よって、この公式から「昇降圧チョッパ」だと分かります。
まとめ
今回説明してきたように、細かな違いのある公式を覚える場合は、導出から覚えておくと頭ごなしに覚える必要がなくなります。チョッパはその典型的な例ですね。
実は今回の解説は2種レベルであったりします。こういった導出もそうですが、電力の知識問題などでも2種のレベルまで掘り下げて始めて納得して理解したことが何度もありました。
そういうところも今後紹介していければと思います。
それでは次回!














ケンタさんおはようございます!
とてもわかりやすいです!
ありがとうございますm(_ _)m
導出から覚えていくというのが興味深かったです。
この記事ではありませんが、コイルに磁石を近づけると電力が発生するなども、導出というか、腑に落ちるまで理解できておくと忘れにくいですよね。
ありがとうございました!
>やまさきさん
コメントありがとうございます。
わかりやすいと言っていただけると素直に嬉しいです。
2日連続の受験頑張ってください!
こんにちは
私が3種を受験したときは、ひたすら公式を丸暗記して答えを求めていました。
それで偶々合格できましたが、電気の本質は全く理解できていません。
2種の場合、公式の導出に関する考え方も求められる様なので、ケンタさんが言われる通り2種を勉強すると電気の事をより理解できると思うし、そうなれば勉強の苦労が理解できる喜びに変わるのかもしれません(とはいっても難解すぎてどこから手を付けて良いかもわかりません。微積分も底なし沼らしいので、電験用に特化しないと)
3種(高校用)と2種(大学用)の違いのように、微積分も高校は公式に当てはめて
答えを求めるけど、大学では本質に近付く為公式の導出から学ぶと聞きました。
いきなり難しい2種の参考書も、今回のケンタさんのように、簡単な図から丁寧に説明してもらえると分かり易いのですが、そうなるとページ数が膨大になるから難しいのかもしれませんね。
何時も、図や公式を描くのに苦労されていると思いますが、
記事をあげて頂いてありがとうございます。
>カモカモさん
コメントありがとうございます!
大学の微積分学では、ε-δ論法(イプシロン-デルタ論法)という周りくどい証明を延々としていた思い出があります。
もうさっぱり忘れてしまいましたが笑
2種の参考書については、私も難解に書いているなぁという印象がありました。
ですので、今回は理解の助けとして私が参考書の余白に書いていた図を持ってきました笑
(一度図を書いてしまえば、コピペ+マイナーチェンジで時間を幾分省略できます笑)
こういった参考書までの橋渡しができるような記事を書いていこうと思います。
これからもおつきあい下さい!
まずタイトル画像で吹きました(笑)
そしてチョッパ回路の公式の導出ですが、私含め多くの3種受験者にとって
ブラックボックスになっている部分を非常に分かりやすく解説して頂いており
すごく良かったです!
実は3種の理論過去問でもパワエレっぽい内容の穴埋め問題が出ており
詳しくは覚えていませんがこの導出内容と似た雰囲気でした!
なので3種受験者も理想的にはここまで理解しておく必要があると思います。
受験前にこの記事を拝見することができ助かりました。
ありがとうございました!
>レベル4さん
コメントありがとうございます!
過去問でこの導出が出たことあったんですね。
知りませんでした。
次は過去問を2問ほど記事にしてみます。
しばしお待ちを!
式の導出が非常に分かりやすかったです。
わざわざ公式を覚えなくても導出の仕方さえ分かっていれば本番でも使えるため参考にさせていただきます。
コメントありがとうございます!
個人的には原理や導出(難しければこじつけでも可)ならば覚えやすいのではないかと思っています。このように,できるだけ丸暗記を避けて学習を進めてくだされば!