皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
今回はレベル4さんからの依頼で、パワーエレクトロニクス(略してパワエレ)の私なりの攻略方法を書いてみようと思います。
今回は前編にあたり、後編では電験3種の過去問2題くらいをテーマに、「私ならこう考えて解く」というのを赤裸々に書いていこうと思います。間違って理解しているというところが多々あるかと思いますが、一例としてお読み下さい。
始めに
パワエレは電験の中でも最も交流と直流の境目に位置していて、時々刻々の直流的な電気的挙動と交流的な電気的挙動をイメージしながら、理解を進める必要があります。
特に、直流的な挙動の方がウェイトは大きいです。ここで、理論で学んだコイルとか電場の理解がきちんとできているかを問われます。
このイメージができれば、
- 記憶するところは最小限に
- 理屈でできるだけ覚える
ということがし易くなるかと思います。語呂合わせで公式を覚えるのが得意な人は、そちらの方で固めるのも手かと思います。が、私のような理屈が気になりだしたら仕方ない人にとっては、きちんと理解して導出できるようになったほうが確実に定着しやすいです。
パワーエレクトロニクス分野の構成
パワエレ分野は主に以下の項目から構成されています。
- パワーデバイスの種類
- 整流回路
- 静止電力変換装置の種類
- 降圧・昇圧チョッパ
パワーデバイスの種類について

ダイオード、サイリスタ、GTO、パワートランジスタ、MOSFET、IGBT
が種類として挙げられます。私は「自己消弧できるか」をポイントとして、覚える際の区分けしています。区分け表を自分で作って覚えるのもいいですが、私にはやはりこじつけでも良いので、理屈で覚えようとする癖があります。
新しい単語を覚える際はカタカナ語であれ英語であれ、腑に落ちるまで意味を調べます。例えば、英語略記されている単語については、毎回必ず略さないとどういう意味なのかというところまで調べます。GTOならば、Gate Turn-Off (thyristor)というようにです。Turn-Offというところから分かるように、GTOは自己消弧機能を持ちます。
また、MOSFETはMetal-Oxide-Semiconductor Field-Effect Transistorの略なので、Field-Effect、つまり電界効果によりゲートを開け閉めすることができることから、自己消弧機能を持つと判断できます。MOSが分からなくても、FETだけは覚えておくと便利です。(MOSはMicrosoft Office Specialistでは無いですよ笑)
IGBTはInsulated Gate Bipolar Transistorの略です。Gate Bipolarというところから、2端子でゲートを開け閉めすることをイメージできます。
整流回路について(単相)
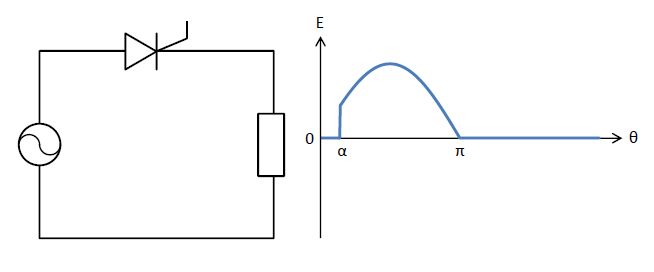
図のようなサイリスタを用いた単相半波整流回路では、コイルが含まれていないので交流電圧\(E\)が負になるときと同じタイミングで、電流も0となり消弧されます。
制御角\(\alpha\)で点弧すると、\(\alpha\leqq\theta\leqq\pi\)の範囲でのみ交流電圧Eが負荷に印加されるとみなせるので、直流電圧\(E_{\mathrm{d}}\)は
\begin{align}E_{\mathrm{d}}&=\frac{印加した交流電圧の全面積}{1周期}\\
&=\frac{\int_\alpha^\pi \sqrt{ 2 }E\sin\theta \mathrm{d}\theta}{2\pi}\\ \end{align}
となります。面積を区間で割ることによって、平均電圧、つまり直流電圧が出てきます。
「道のり・速さ・時間」に例えると、分子は「速さ×時間」つまり、道のりに相当します。分母は時間に相当するので、結果として分数全体では「速さ」になります。
私は、この積分の組み立て方を覚えていました。理由は積分した結果の
\begin{align}E_{\mathrm{d}}&=0.45E\frac{1+\cos\alpha}{2}\\ \end{align}
だけを覚え続けるのは直感的に不可能だと感じたからです。導出の方法を覚えて試験時間に余裕があれば、この式を覚えておかなくてよくなります。この導出ができるようになれば、三相交流回路の半波整流回路でも同じように直流電圧を導出することができます。
整流回路の単元では色んな直交変換公式が出てくるので、この組み立て方を1つだけ覚えるようにして省エネをしていました。
なお、全波整流回路については、1周期の面積が単純に2倍になるので、半波整流回路の2倍の直流電圧になります。
整流回路について(三相)
三相半波整流回路は三相交流回路の電圧のグラフがかければ、単相交流と同じように直流電圧を導出することができます。
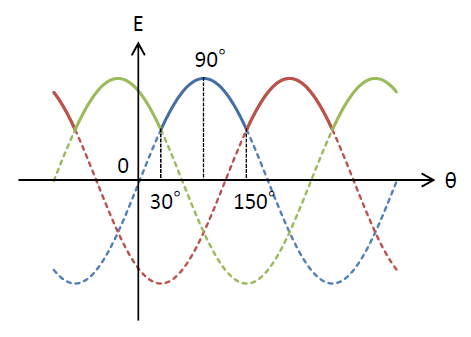
先ずはグラフの書き方から。
書く際に抑える箇所としては、120°ずつ出力する電源が変わるということです。
青のグラフが1番始めに書くメインのsinのグラフです。\(\theta=0°\)で\(E=0\)となるグラフです。\(\theta=90°\)で最大となり、青が出力できるのは前後60°ずつなので、青の出力範囲は\(30°\leqq\theta\leqq 150°\)となります。
これで、青の実線部分が書けます。
ただ、この書き方をしていると、青の出力範囲を0から考えて\(30°\leqq\theta\leqq 150°\)を導き出すのと、その後の積分が面倒なので、私は以下のような図に書き直しています。
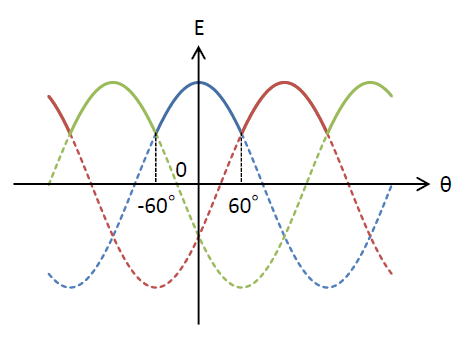
青の出力範囲を\(-60°\leqq\theta\leqq 60°\)とします。公式の分子は面積を計算しているので、積分区間がどうであろうと同じ形の部分を積分するならば、積分区間の設定の仕方は問題とはなりません。
こうすることで公式を
\begin{align}E_{\mathrm{d}}&= \frac{\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}} \sqrt{ 2 }E\cos\theta \mathrm{d}\theta}{\frac{2}{3}\pi}\\ \end{align}
とすることができます。赤と緑の部分は繰り返し部分となりますので、\(2\pi\)の区間で積分しても、上式の積分をしても答えは同じになります。
静止電力変換装置の種類について
ここはもう覚えるしかありません。
サイクロコンバータは、可変速揚水発電システムに使われています。揚水ポンプの速度を変えて運転することで、電力系統の細かな需給調整(周波数調整)に使えます。ポンプを誘導機で可変速運転させるときに、2次側の滑り周波数を自在に変える必要があり、サイクロコンバータを使ってこの微妙な低速周波数変化をさせています。
また、この分野ではよく「PWM制御方式」という単語が出題されます。直交変換する際の制御方式の1つです。
降圧・昇圧チョッパ
ここが私的に1番説明ボリュームが大きいところです。
大きすぎるのでここは次回にしたいと思います。
まとめ
このブログを開設して、1番それっぽい記事なりましたね笑
一部端折ったところもあるものの、概ねこんな感じに私は理解しています。
次回ではチョッパのお話をして、次々回ではこの理解をどう過去問の誘導に合わせて解答していくかを書いていく予定です。
それでは次回!
https://den1-tanaoroshi.com/chopper-in-powerelectronics[/chat]















記事読ませて頂きました!
整流回路についてですが、直流平均電圧Edを求める問題など
具体的な値を求める場合は、やはり積分ができないと本質的に理解できない
ということですね。
情けない話ですが、私は高校でやったはずの積分を全く覚えていませんので
まず積分の勉強からとなると、それだけで結構な時間がかかりそうですし
覚えることも多そうです。
ですので整流回路に関しては
半波、全波(コイル有り無し)、三相全波の4種類の積分した結果を丸暗記して
使い分けることで対応しようと思います。
今回、私は3種初受験ですがゆくゆくは2種も視野に入れており
その時は積分をさけて通れないだろうなと思いました。
(当分先になりそうですが)
ためになる記事ありがとうございました。
チョッパ回路の記事も楽しみにしております!
>レベル4さん
幾らかためになることが書けたようで何よりです!
積分は確かに避けて通れないですね。
計算もそうですが微小区間の考え方ができるようになると、2種二次試験の配電線路の電圧降下などの問題とか、一次理論のガウスの法則とかが比較的楽に解けるようになります。
微積は2種のごく一要素ですので、2種の勉強では微分方程式とかの実際の計算は優先度低めで構わないと思います!
いいです。解りやすいです。
特に基本的な考え方が解りやすいです。
図は面倒であれば、手書きのもを写真で取っただけでも良いと思います。
きれいな図は、出版するときに出版社に作ってもらいましょw
>ハゲおっさんさん
ありがとうございます!
パワエレの個別の概念図とか積分の概念図とかパワポで書こうとしたのですが、面倒だったので諦めました笑
案の定そこを突っ込まれたので、チョッパー編の前にこの記事を加筆しておきます。
ゆくゆくのことは置いておいて、こういう記事は書き貯めていきたいですね笑
続きよろしくお願いします。自分も1種まで所得を目指していて、読んでいてとてもためになっています。
>マグロハンターさん
コメントありがとうございます!
そう言ってくださると励みになります!
最近(ビルメンにしては)忙しいので、チョッパー編は早くて来週あたりになりそうですが、しばしお待ちください。
書いて欲しいネタがありましたらご希望受け付けます!