皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
半年程前に電験2種 過渡現象をラプラス変換で解く24年間 平成30年度版の販売を告知させていただきました。それにあたっていただいたコメントに
ラプラス変換を使わずとも簡易式というのがあります。
というのがありました。
それを受けて今回、その簡易式を別解としてラプラス変換本のボリュームアップを実行しました!

過渡現象における簡易式とは
電流\(i(t)\)、電圧\(v(t)\)、電荷\(q(t)\)それぞれについて、
\begin{align}i(t)&=i(\infty)+\{ i(0)-i(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
v(t)&=v(\infty)+\{ v(0)-v(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
q(t)&=q(\infty)+\{ q(0)-q(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
\end{align}
に初期値(\(i(0)\)など)と定常値(\(i(\infty)\)など)、時定数\(\tau\)に数値や文字を代入すれば、確かにラプラス変換をせずに簡単に求まります。
この簡易式は結果的には正しいのですが、これだけ提示されて正しいと言われても、狐につままれた感が拭えないと思いますので、導出をしてみます。
導出方法
導出する前に、この簡易式は\(\boldsymbol{RL}\)回路・\(\boldsymbol{RC}\)回路に限る話となります。
2つの回路について、知りたい地点の電流\(i(t)\)、電圧\(v(t)\)、電荷\(q(t)\)を求めることができます。
\(RL\)回路
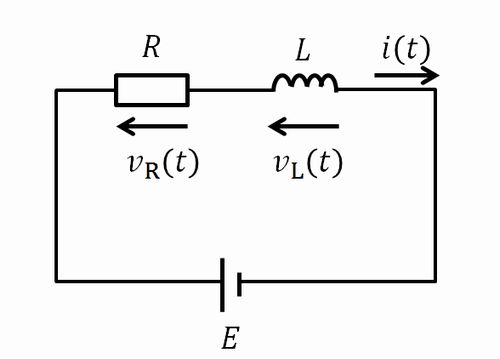
電流\(i(t)\)の導出
回路全体について微分方程式を立てると
\begin{align}Ri(t)+L\frac{\mathrm{d}i(t)}{\mathrm{d}t}=E\\ \end{align}
となります。この形の微分方程式は、過渡解と定常解に分けて求めて、重ね合わせて一般解を求めます。
過渡解は、積分定数Cと定数Aを用いて以下のように求まります。
\begin{align}Ri(t)+L\frac{\mathrm{d}i(t)}{\mathrm{d}t}&=0\\
L\frac{\mathrm{d}i(t)}{\mathrm{d}t}&=-Ri(t)\\
\frac{\mathrm{d}i(t)}{i(t)}&=-\frac{R}{L}\mathrm{d}t\\
\mathrm{ln}\ i(t)&=-\frac{R}{L}t+C\\
i(t)&=\mathrm{e}^{-\frac{R}{L}t+C}\\
&=A\mathrm{e}^{-\frac{R}{L}t}\\
\end{align}
定常解は\(E\)や\(R\)で表記することも可能ですが、簡易式の完成形を見越して\(i(\infty)\)の表記のままとします。
以上より、一般解は
\begin{align}i(t)&=A\mathrm{e}^{-\frac{R}{L}t}+i(\infty)\\ \end{align}
となります。一般解の初期値を\(i(0)\)とすると、
\begin{align}i(0)&=A\mathrm{e}^{0}+i(\infty)\\
\therefore A&=i(0)-i(\infty)\\ \end{align}
となります。
したがって、\(\frac{L}{R}\)を時定数\(\tau\)に置き換えると、
\begin{align}i(t)&=i(\infty)+\{ i(0)-i(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
\end{align}
が求まります。
電圧\(v(t)\)の導出
\(v_\mathrm{L}(t)\):コイルの電圧
\begin{align}v_\mathrm{R}(t)&=i(t)R\\
&=i(\infty)R+\{ i(0)R-i(\infty)R \} \mathrm{e}^{-\frac{t}{\tau}}\\
&=v_\mathrm{R}(\infty)+\{ v_\mathrm{R}(0)-v_\mathrm{R}(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
v_\mathrm{L}(t)&=E-v_\mathrm{R}\\
&=\{E-v_\mathrm{R}(\infty)\}-\{ v_\mathrm{R}(0)-v_\mathrm{R}(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
&=v_\mathrm{L}(\infty)+\{ -v_\mathrm{R}(0)+v_\mathrm{R}(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
&=v_\mathrm{L}(\infty)+\{ E-v_\mathrm{R}(0)-E+v_\mathrm{R}(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
&=v_\mathrm{L}(\infty)+[ \{E-v_\mathrm{R}(0)\}-\{E-v_\mathrm{R}(\infty)\} ] \mathrm{e}^{-\frac{t}{\tau}}\\
&=v_\mathrm{L}(\infty)+\{ v_\mathrm{L}(0)-v_\mathrm{L}(\infty)\} \mathrm{e}^{-\frac{t}{\tau}}\\
\end{align}
\(RC\)回路
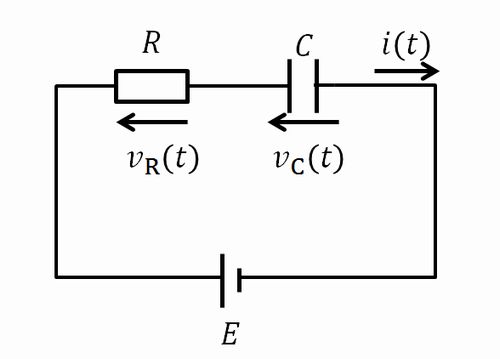
電流\(i(t)\)の導出
回路全体について電圧降下の式を立てると
\begin{align}Ri(t)+v_\mathrm{C}(t)=E …(1)\\ \end{align}
となります。
一方で、コンデンサにおける電荷\(q(t)\)は定義より
\begin{align}\displaystyle \int ^t _0 i(t)\mathrm{d}t& \equiv q(t)\\
&=Cv_\mathrm{C}(t)\\
\end{align}
つまり、両辺を微分して
\begin{align} i(t)&=C\frac{\mathrm{d}v_\mathrm{C}(t)}{\mathrm{d}t}\\
\therefore \frac{\mathrm{d}v_\mathrm{C}(t)}{\mathrm{d}t}&=\frac{i(t)}{C}\
\end{align}
となります。これを式(1)の両辺を微分した式に代入して
\begin{align}R\frac{\mathrm{d}i(t)}{\mathrm{d}t}+\frac{i(t)}{C}&=0\\
\frac{\mathrm{d}i(t)}{i(t)}&=-\frac{\mathrm{d}t}{CR}\\
\mathrm{ln}\ i(t)&=-\frac{t}{CR}+C\\
i(t)&=\mathrm{e}^{-\frac{t}{CR}+C}\\
&=A\mathrm{e}^{-\frac{t}{CR}}\\
\end{align}
\(t=0\)のとき
\begin{align}i(0)&=A\mathrm{e}^{0}\\
\therefore A&=i(0)\\
\end{align}
また、\(t\to 0\)のとき
\begin{align}i(\infty)&=A\times 0\\
&=0\\
\end{align}
以上より、\(CR\)を時定数\(\tau\)に置き換えたうえで、簡易式に揃えるように\(i(t)\)を式変形をしていくと
\begin{align}i(t)&=i(0)\mathrm{e}^{-\frac{t}{\tau}}\\
&=0+{i(0)-0}\mathrm{e}^{-\frac{t}{\tau}}\\
&=i(\infty)+\{ i(0)-i(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
\end{align}
が求まります。
電圧\(v(t)\)の導出
\(v_\mathrm{C}(t)\):コンデンサの電圧
\begin{align}v_\mathrm{R}(t)&=i(t)R\\
&=i(\infty)R+\{ i(0)R-i(\infty)R \} \mathrm{e}^{-\frac{t}{\tau}}\\
&=v_\mathrm{R}(\infty)+{ v_\mathrm{R}(0)-v_\mathrm{R}(\infty) } \mathrm{e}^{-\frac{t}{\tau}}\\
v_\mathrm{C}(t)&=E-v_\mathrm{R}\\
&=\{E-v_\mathrm{R}(\infty)\}-\{ v_\mathrm{R}(0)-v_\mathrm{R}(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
&=v_\mathrm{C}(\infty)+\{ -v_\mathrm{R}(0)+v_\mathrm{R}(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
&=v_\mathrm{C}(\infty)+\{ E-v_\mathrm{R}(0)-E+v_\mathrm{R}(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
&=v_\mathrm{C}(\infty)+[ \{E-v_\mathrm{R}(0)\}-\{E-v_\mathrm{R}(\infty)\} ] \mathrm{e}^{-\frac{t}{\tau}}\\
&=v_\mathrm{C}(\infty)+\{ v_\mathrm{C}(0)-v_\mathrm{C}(\infty)\} \mathrm{e}^{-\frac{t}{\tau}}\\
\end{align}
電荷\(q(t)\)の導出
\begin{align}q(t)&=Cv_\mathrm{C}(t)\\
&=Cv_\mathrm{C}(\infty)+\{ Cv_\mathrm{C}(0)-Cv_\mathrm{C}(\infty)\} \mathrm{e}^{-\frac{t}{\tau}}\\
&=q(\infty)+\{ q(0)-q(\infty)\} \mathrm{e}^{-\frac{t}{\tau}}\\
\end{align}
感覚的な導出
簡易式があるのは覚えているけどその導出の仕方を忘れてしまったときは、感覚的な導出で乗り切る方法もあります。
まず、電流であろうと電圧であろうと電荷であろうと、式の形は全部同じということだけは飲み込みます。
\begin{align}i(t)&=i(\infty)+\{ i(0)-i(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
v(t)&=v(\infty)+\{ v(0)-v(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
q(t)&=q(\infty)+\{ q(0)-q(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
\end{align}
次に、単純な減衰関数を余白に書きます。

このグラフから\(i(t)\)の簡易式を作っていきます。

このようにベース部分と減衰部分に切り分けます。
ベース部分は\(i(\infty)\)です。
減衰部分は自然対数の底\(\boldsymbol{\mathrm{e}}\)で減衰していくとします。
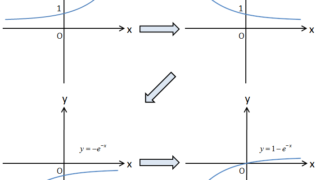
ということで、初期量\(i(0)-i(\infty)\)が減衰していきますので、
\begin{align}\{ i(0)-i(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\ \end{align}
と表せます。
以上、2つを合わせると
\begin{align}i(t)&=i(\infty)+\{ i(0)-i(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
\end{align}
となります。
ということで、\(v(t)\)も\(q(t)\)同じ形の
\begin{align}v(t)&=v(\infty)+\{ v(0)-v(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
q(t)&=q(\infty)+\{ q(0)-q(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
\end{align}
となります。
実際の使用例
実際に簡単な回路を使って、例題を解いてみましょう。なお、電流・電圧・電荷全てを書くのは面倒ですので笑、電流だけを求めてみます。
\(RL\)回路

コイルの特性から
\begin{align}i(0)=0, i(\infty)=\frac{E}{R}\\ \end{align}
となりますので、簡易式に代入して
\begin{align}i(t)&=i(\infty)+\{ i(0)-i(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
&=\frac{E}{R}+\{0-\frac{E}{R} \} \mathrm{e}^{-\frac{R}{L}t}\\
&=\frac{E}{R}(1-\mathrm{e}^{-\frac{R}{L}t})\\
\end{align}
となります。
\(RC\)回路
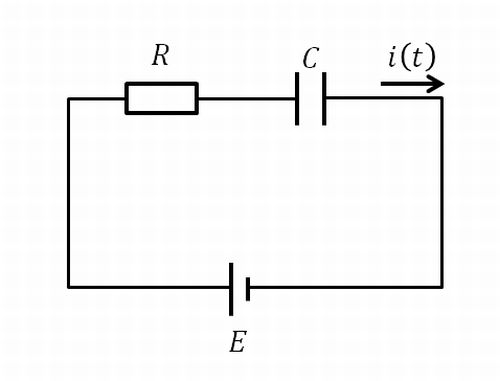
コンデンサの特性から
\begin{align}i(0)=\frac{E}{R}, i(\infty)=0\\ \end{align}
となりますので、簡易式に代入して
\begin{align}i(t)&=i(\infty)+\{ i(0)-i(\infty) \} \mathrm{e}^{-\frac{t}{\tau}}\\
&=0+\{\frac{E}{R}-0 \} \mathrm{e}^{-\frac{t}{CR}}\\
&=\frac{E}{R} \mathrm{e}^{-\frac{t}{CR}}\\
\end{align}
となります。
まとめ
このように、本来であれば微分方程式を立てて解くところ、簡易式を使えば一気に最後までショートカットできるようになります。
私としては電験1種で必須となってくるラプラス変換の解法も捨てがたいのですが、事実として簡易式の方も確かに楽ですので、ご紹介しました。

お好きな方を!それでは次回!













たびたびすいません。
簡易式は「i(t)=i(∞)+(i(0)-i(∞))exp(-t/τ)」等ではありませんか。「i(t)=i(∞)+i(0)-i(∞)exp(-t/τ)」という表記だと、「i(t)=i(∞)+i(0)-(i(∞)exp(-t/τ))」という意味になってしまいます。
最初はそういうものかと思っただけでしたが、貴サイトを何周か見て回っているうちに過渡現象がわかり始めて、気が付きました。
>Tomさん
ご指摘の通りで修正しましす。失礼しました。(数式表示の仕様変更で{ }が非表示になってしまっていました)
あってはならないことですが、間違いに気付けるほど習熟されてきたということで…
道理で。貴サイトにしては単純ミスで、どこからチェック無しでコピーしてきたかと思ってしまいました。
しばらくは、貴サイトを含めたラプラスと制御関係のページを回って、学習を進めようかと思っています。