皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
半年程前に電験2種 過渡現象をラプラス変換で解く24年間 平成30年度版の販売を告知させていただきました。そこから色々あり、ページ数的には20%ほど加筆・修正をしまして、第2版として再販売することになりました!


クレーム(?)的なものもあり

私としては、過渡現象をラプラス変換で解けるというのは提案の1つということで紹介したつもりでしたが、\(\boldsymbol{RL}\)回路・\(\boldsymbol{RC}\)回路に限ればもっと簡単な解法があるというコメントをいただきました。
それは、解法というか、ある簡易式に代入すれば答えが出るものでした。
電流\(i(t)\)、電圧\(v(t)\)、電荷\(q(t)\)それぞれについて、
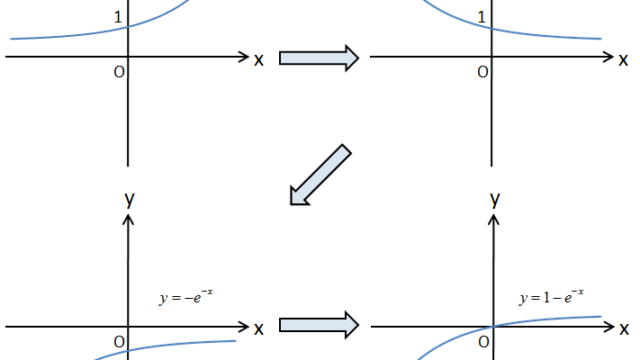
\begin{align}i(t)&=i(\infty)+{ i(0)-i(\infty) } \mathrm{e}^{-\frac{t}{\tau}}\\
v(t)&=v(\infty)+{ v(0)-v(\infty) } \mathrm{e}^{-\frac{t}{\tau}}\\
q(t)&=q(\infty)+{ q(0)-q(\infty) } \mathrm{e}^{-\frac{t}{\tau}}\\
\end{align}
に初期値(\(i(0)\)など)と定常値(\(i(\infty)\)など)、時定数\(\tau\)に数値や文字を代入すれば、確かにラプラス変換をせずに簡単に求まることができます。

ということで、この解法を別解として解説に追加しました。
2種では悪手のハズが1種ではなくてはならない解法となる
過渡現象をラプラス変換で解く方法は、二次試験の内容を先取り・変形適用していますので、一次試験までに一次試験の4科目しか準備する時間がない方にとっては、時間的な余裕がありません。また、時間があっても電力・機械・法規の完成度が甘い場合は、そちらの理解度を上げる方を優先させた方が無難です。
が、電験1種を最終目標にしている方でしたら、このタイミングでラプラス変換で解く解法をマスターしておいて損はありません。

電験1種では一次試験をそこそこに、二次試験の準備をどれだけこなせるかが重要だと思いますので、先取り学習をしてはどうでしょうか。
購入者からのありがたいご指摘

また、ラプラス変換本を購入してくださった者から、誤植に関するご指摘をいただきました。
独りで作っていたので…というのを理由にしたくはないですが、指摘量が多く他の購入者にも迷惑をかけていたのかと思うと、大変申し訳ない気持ちになりました。
既に購入された方はメールアドレスを把握していますので、第2版のPDFを遅らせていただきました。
販売ルートを増やしました

- 別解を充実させて
- 誤植を(見つけた限りで)潰した
ことで一区切り点きましたので、販売ルートのテコ入れをしました。
これまでは、委託販売サイトのstore.jpからしか購入することができませんでしたが、加えて第2版からは巨人の力を借りようと思います。
巨人の名はAmazonです。
巨人に再挑戦
Amazonでは、以前Kindle unlimitedという電子書籍サービスに挑戦したことがありました。
しかし、WordとPowerPointで作成したラプラス変換本のPDFは、電子書籍への変換がうまく行かず、仕方なく断念したのです。
今回はPOD(Print on Demand)ということで、Amazonで注文すると紙媒体(ペーパーバック)としてAmazonとは別の業者が印刷したものが届くことになります。PDFでの販売と違って印刷の手間が省けますし、持ち運びやすいかと思います。
そして何より、Amazonの検索に引っかかるようになりますので、比べるまでもなく多くの人の目に触れるようになります!これは大きい!
PDF版は値下げ!
商売の素人の私にとって、モノの値段を設定するのは大変でした。
値段の付け方を間違ったせいか、そもそもターゲッティングが悪かったのかPDF版の売れ行きはあまりよろしくありません。
ということで、今回ペーパーバックを販売したのに合わせて、PDF版を値下げすることにしました!

まとめ
初版を発売してから色々とありましたが、それでもめげずに第2版を発売することができました。
- 別解を充実させて
- 誤植を(見つけた限りで)潰した
これらの改善を踏まえて今回からAmazonでのペーパーバック販売も拡充してみました。
それでは次回!















先ほどは失礼しました。
良く読み返したら、前購入者にはメールで
第2版を送付してくださるとの事、ありがとうございます。
先ほどのコメントは削除してください。
>カモカモさん
お久しぶりです!
お気付きの通り、購入時に登録したアドレスに送信しています。
届いていなければ、そのアドレスを使ってページ下の問合せよりコンタクトしてください。
そこに再送します。
おはようございます!
第2版を購入して2週間程で25%の値下げ…
まぁ、勉強を2週間先行したということで良しとします(笑
理論のテーマ別過去問(平成7年~19年)を3周くらいしましたが、過渡現象が意味が分からず鬼門でした。理解していないので久々にやるとチンプンカンプンでしたし。。。
でも、お陰様でラプラス変換や分数展開の理解が深まり、レベル2もちょいちょい解けるようになってきました。
別解も分かりやすいのですが、まずは王道?のラプラス変換で解くようにしています。
>ソウケイさん
お久しぶりです!
ご購入ありがとうございます。
タイミングが悪かったですね汗
是非使い倒してください!
あとなにか気になることがあればメールください。
御世話になります。以前、初版を購入したのですが、メールが消失して、資料をどこに置いたか分からなくなりました。いつの間にか第2版が出したことですが、購入可能でしょうか?
>tabitetuさん
コメントありがとうございます。
Twitterの方にダイレクトメールを送らせていただきました。
そちらをご確認ください。