皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
少し前に、「ラプラス変換で新制度(平成7年度)以降の過渡現象問題を解いて、それを販売します。」という記事を書きました。

それを無事作り終えましたので、感想などを記事にしてみました。
過渡現象問題の出題頻度
過渡現象が電験2種一次試験理論の最大の壁となる人は多いと思います。
平成7年度に試験制度が新制度になってから平成29年度までに23回試験が行われている中で、過渡現象はなんと21回出題されています。ということで、過渡現象を完答できるかできないかで、試験の合否が決まる可能性が高いです。
しかも、
- ラプラス変換で解いたほうが近道だった
- 少なくとも微分方程式と解くスピードが変わらない
年度が9割近くでした。
どうやら↓の年度のような、微分方程式で解いたほうがマシという年度はとてもマイナーのようです。

平成25年度前後の難易度が明らかに高い


コチラの記事では、平成25年度の過去問をラプラス変換で解いていました。
このときはラプラス変換よりかは過渡現象で解いた方が
- 穴埋めに沿った計算ができる
- (どちらにしろ多いけど比較的)計算量を抑えられる
ということを述べていました。でも、微分方程式で解いても相当の計算量だったんです。
今回、この前後の年度もラプラス変換で解いてみたのですが、平成25年度前後は明らかに過渡現象で受験者を落としにかかっている印象を受けました。過渡現象が苦手でこの年度に受験した方は本当に大変だったと思います。
初期条件が意外と必要

\(t=0\)の時点で
- コンデンサが充電されていたり
- コイルに電流が流れている
という条件が意外と頻出でした。
割合としては10/21年度で、約2回に1回です。
微分方程式の方では簡単に初期条件を適用することができますが、ラプラス変換の方も知っていれば簡単に適用することができます。ということで、この場を使って解説しておきます。
なお、数学的に説明した過去記事も合わせて御覧下さい。
コンデンサの初期条件
コンデンサに電荷が溜まっていくと、電源に対して抵抗する方向に電圧(逆起電力)が発生していきます。この方向に気を付けて、\(t\)回路から\(s\)回路に変換していきます。
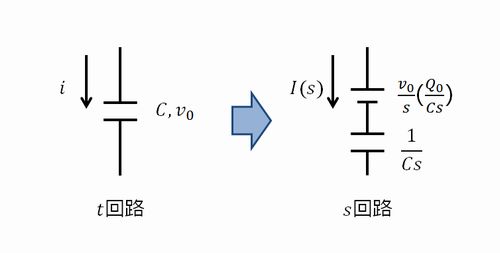
初期条件部分は、定電圧電源のラプラス変換と全く同じであることが分かるかと思います。
\(v_0\)が分からないときは、\(Q=Cv\)の関係から\(\frac{Q_0}{Cs}\)を逆起電力として\(s\)回路に表記すれば問題ありません。
コイルの初期条件
\(t=0\)でコイルに電流が流れているときは、コイルとしては電源に加勢するように電圧を発生させます。ということで、それを\(s\)回路に表記すると↓のようになります。
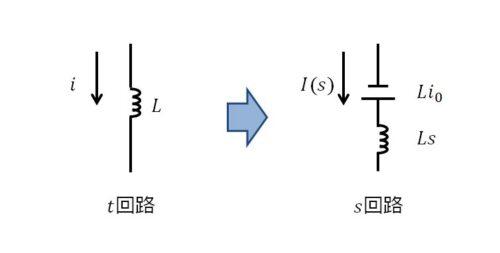
部分積分を使うことになるとは…
ラプラス変換で部分積分を使うことになるとは思いませんでした…正確に言うと、微分方程式で解いていても部分積分をすることになる問題でしたので、どちらにしろ面倒なことにはなります笑
計算量・レベル共に電験2種では悪い意味でピカイチですので、仕切り直して次々回で公式の説明から詳しく書きます。
まとめ
新制度以降の問題を全て解いてみてみて、ラプラス変換が過渡現象にとても有効であることが分かりました。
ラプラス変換は二次試験の機械・制御でどちらにしろ必要になってきますので、一次試験理論のタイミングで使えるようになっておくと、機械・制御に加えて理論でも使える武器にしておけます。
皆さんも是非ラプラス変換を使った過渡現象に挑戦してみて下さい!
それでは次回!