電験２種に四次方程式の解の公式が登場してくる？！

皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。

世の中はゴールデンウィークですね。ふらっと立ち寄ったお店で「GOLDEN WEEK」という販促ポスターを見かけたのですが、和製カタカナ英語をアルファベット表記していることに強い違和感を覚えました笑

ゴールデンウィークでも私は相も変わらずブログを更新しているわけですが、実はネガティブでない諸々の事情により暫くブログ更新を休止するとtwitterの方では告知していました。が、少し時間ができましたので更新します笑

2週間ほど前に電験２種二次試験の送電問題について読者の方から質問をいただきましたので、今回はその解説をします。

四次方程式を解く？

問題をお持ちでない方でも解説が分かるように、簡素化してはじめから説明をしていきます。

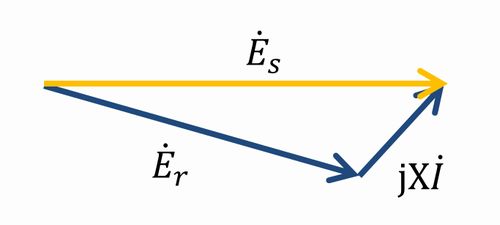
受電端相電圧\(E_\mathrm{r}\)と線路のインダクタンス\(X\)、負荷の有効電力\(P\)と無効電力\(Q\)（遅相無効電力を正）がわかっているときに、送電端相電圧\(E_\mathrm{s}\)を求める問題です。

求める途中に四次方程式が出てくるため、式展開が分からないというご質問でした。

先ず、一般的に以下の関係が成り立ちます。

\(\dot{E_\mathrm{s}}=\dot{E_\mathrm{r}}+\mathrm{j}X\dot{I}\)　　　　  式①

\(P+\mathrm{j}Q=3\dot{E_\mathrm{r}}\overline{\dot{I}}\)　　　　　式②

共役を感覚的に使い分けて複素電力を求めてみよう皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。 専門用語ばかりのタイトルになってしまい、何についての記事を...

ここで式②より

\begin{align}\overline{\dot{I}}&=\frac{P+\mathrm{j}Q}{3\dot{E_\mathrm{r}}}\\
\dot{I}&=\frac{P-\mathrm{j}Q}{3E_\mathrm{r}}\\ \end{align}

これを式①に代入して

\begin{align}\dot{E_\mathrm{s}}&=E_\mathrm{r}+\mathrm{j}X\times\frac{P-\mathrm{j}Q}{3E_\mathrm{r}}\\
&=\left(E_\mathrm{r}+\frac{XQ}{3E_\mathrm{r}}\right)+\mathrm{j}\frac{XP}{3E_\mathrm{r}}\\
E_\mathrm{s}^2&=\left(E_\mathrm{r}+\frac{XQ}{3E_\mathrm{r}}\right)^2+\left(\frac{XP}{3E_\mathrm{r}}\right)^2\\
&=E_\mathrm{r}^2+\frac{2XQ}{3}+\left(\frac{XQ}{3E_\mathrm{r}}\right)^2+\left(\frac{XP}{3E_\mathrm{r}}\right)^2\\
&=E_\mathrm{r}^2+\frac{2XQ}{3}+\left(\frac{X}{3E_\mathrm{r}}\right)^2(P^2+Q^2)\\
\end{align}

ここで送電端線間電圧を\(V_\mathrm{s}\)、受電端線間電圧を\(V_\mathrm{r}\)とすると、

\begin{align}\left(\frac{V_\mathrm{s}}{\sqrt{3}}\right)^2&=\left(\frac{V_\mathrm{r}}{\sqrt{3}}\right)^2+\frac{2XQ}{3}+\left(\frac{X}{\sqrt{3}V_\mathrm{r}}\right)^2(P^2+Q^2)\\
\end{align}

となります。

求めたい値は\(V_\mathrm{r}\)ですので、\(V_\mathrm{r}\)をメインに整理していきます。

\begin{align}\frac{V_\mathrm{s}^2}{3}&=\frac{V_\mathrm{r}^2}{3}+\frac{2XQ}{3}+\frac{X^2}{3V_\mathrm{r}^2}(P^2+Q^2)\\
V_\mathrm{s}^2V_\mathrm{r}^2&=V_\mathrm{r}^4+2XQV_\mathrm{r}^2+X^2(P^2+Q^2)\\
V_\mathrm{r}^4&+(2XQ-V_\mathrm{s}^2)V_\mathrm{r}^2+X^2(P^2+Q^2)=0\\
\end{align}

ここでようやく四次方程式が登場してきます。

四次方程式は見かけだけ

見方を変えると、実はニ次方程式だということが分かります。

\(x=V_\mathrm{r}^2,b=2XQ-V_\mathrm{s}^2,c=X^2(P^2+Q^2)\)とすれば先程の式は

\begin{align}x^2+bx+c=0\\
\end{align}

となります。ということで、解の公式が使えて

\begin{align}x&=\frac{-b\pm\sqrt{b^2-4c}}{2}\\
V_\mathrm{r}^2&=\frac{-(2XQ-V_\mathrm{s}^2)\pm\sqrt{(2XQ-V_\mathrm{s}^2)^2-4X^2(P^2+Q^2)}}{2}\\
V_\mathrm{r}&=\sqrt{\frac{-(2XQ-V_\mathrm{s}^2)\pm\sqrt{(2XQ-V_\mathrm{s}^2)^2-4X^2(P^2+Q^2)}}{2}}\\
&=\sqrt{\frac{V_\mathrm{s}^2-2XQ\pm\sqrt{(V_\mathrm{s}^2-2XQ)^2-4X^2(P^2+Q^2)}}{2}}\\
\end{align}

となります。

まとめ

今回は解の公式が出てくることになって、計算量の多い問題でした。

試験問題としてはこのあと、最後の式の\(V_\mathrm{r}\)、\(X\)、\(P\)、\(Q\)に具体的な数値を代入していくことになります。そうなってくると正に電卓の機能を駆使できているかが問われてきます。

確実に計算をこなして完答できるように、電卓の機能を把握しておきましょう。このくらいの計算であれば電卓のみで計算が可能です。

試験会場に持ち込める『最強の武器』皆さまお疲れさまです。ケンタ（@den1_tanaoroshi）です。 試験勉強をするにあたって、日々の勉強セットを固めている人は...

それ以外のポイントとしては式①②を覚えておくということでしょうか。

この式は結構頻出です。

それでは次回！