皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
試験前で根を詰めているところに、バカげたお話はいかがでしょうか笑
これから書く記事ネタは少し前から考えていたものです。が、あまりにしょうもないので、試験直前まで記事にするか迷っていました。
ネタのオチを確かめる労力ももったいなかったので、確かめもせずにこの時期まで延ばしてきたものです。あとはネタの内容的に、試験問題の印刷出稿が終わって手戻りができなくなってから書いてやろうと思ったのもあります。
オチ次第では(そんなこと有るはずがないですが)試験センターがびっくりして、試験問題を変えるのかもと妄想をしていましたし。
そのネタとは?
ネタをばらす前に少し昔話を。
センター試験というものがあり…

私は大学受験時にセンター試験というものを経験してきています。
2020年にはセンター試験が廃止されてTOEIC的な英語試験を活用したり、それ以外の科目では全国共通の筆記試験にしたりとかと色々話がありますが、私が受験生だったときは古き良き(?)マーク式の試験でした。
センター試験も電験と同じでマーク式なんですよね。国語は全部選択式で、数学はエネルギー管理士の計算問題みたいなマーク式でした確か。
で、受験時に同級生の中で少し話題になったのが、
「センター試験のマークって、どれを選べば確率的に当たりやすいんだ?」
ってやつです。
バカバカしくて調べる気にもなりませんでしたし、もし有るのならば受験業界ですぐに話題になり、センター試験製作側もすぐに対処していたことでしょう。
そうです。勘の良い方はもう気付いたでしょう。
今回は、電験で同じことを検証してみました!?
今回の検証テーマ
「選択肢を絞れずに困った場合は、どの数字を選べばまぐれでも正解になるのか?」
が今回のテーマです。
前回までの真面目な記事との落差が大きいですね笑 すみません。
毎回、図と数式を書いていると疲れるので、今回は文章メインとさせて下さい笑
使用したデータ
- 電験3種の科目別解答(過去5年分)
を材料に、わかりやすさ重視で
- この科目ならこの数字を選んでおけば取り敢えずOK
というのを言えるように分析しました。点数による加重を考慮していません。(A問題もB問題も同じカウントということです。)
なお、試験で実行するかは自己責任でお願い致します。(←当たり前ですが)
検証結果
理論
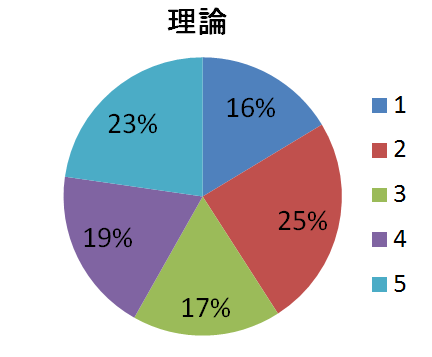
んー、早速ですが微妙ですね笑
2を選んでおけばいいのか?という程度ですね。
電力
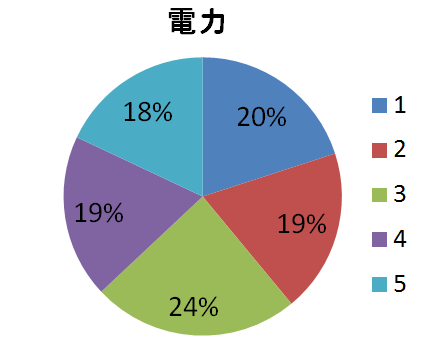
これまた微妙ですね。
やはり試験センターも考えていますね笑
3かなぁ
機械
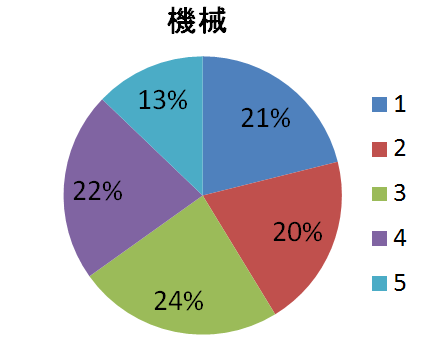
5は選ばない方がいいかもしれませんね。
法規
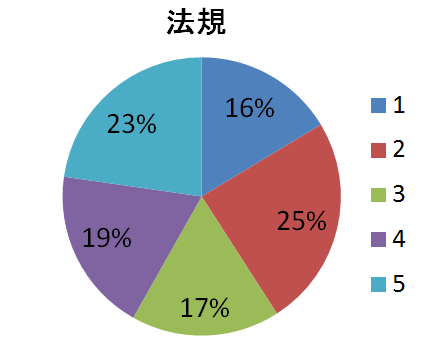
私でしたら2か4を選びます。
まとめ
検証する前から分かりきっていたことですが、やはり明確な推しはできませんね笑 申し訳ないです。
統計的に見事に分散していないとおかしいですもんね。
ご自身で選択肢を絞った後で、どうしても最後の2択が選べないというときに……いや、止めて下さい。責任取れません汗
試験開始前に緊張してきたときは、変なブログで変な管理人が変なことを記事にしていたな、というのを思い出してリラックスするのにでも使っていただけたら幸いです。
それでは次回!















ケンタさんこんばんは!
難しいまじめな記事が続いていましたので、アカデミックな清涼剤的記事、ありがとうございます(^ ^)
どんなオチが待っているのかドキドキでしたがまさかの展開おもしろかったです。
ケンタさんにしか書けない記事ですね。
またこのような記事楽しみに(?)しています!
>やまさきさん
コメントありがとうございます!
今後はもう少しまともな記事を書きます笑
理論28年15の解説ありがとうございました!頑張ります
あちらでなぜがコメントできずこちらにしました
>コンボイさん
コメントありがとうございます!
コメント禁止制限をしていなかったのですが? おかしいですね。
なにはともあれ読んでいただけたようでなりよりです!
こんばんは~
このネタ、前に別のとこで見たことがありますね・・・
そこで見た情報だと計算問題と非計算問題に関しては正解の選択肢の位置の存在確率が偏っていたというものでした。ただし理論に限ってはその傾向が見られないって感じでしたね。計算問題では正解を端に配置すると選択肢の作成が窮屈になるとかいう理由づけがされてましたね。
まぁこれはアレですが・・・受験者間隔の取り方がセンター試験等に比べて甘いため意図してなくても近くのマークシートが見えてしまうことがあるんですよね^^;(前後で1列あけてないことが多い)
合格率が低い試験なので正答率は低いですが、それでもランダムよりは確率が高い(大体40%ぐらいか)
>hiroさん
コメントありがとうございます!
この記事を書いてから私も検索したのですが、細かな分析をしているところもあるのを知りました汗
でも私が言いたかったのは『この科目だったらこの数字』というシンプルなレベルだったので、不発に終わった次第です。
数値問題 or notとかA問題 or notとかの要素を入れて、試験開始直前に読者さんを混乱させても本末転倒と感じたので笑
しょーもないですが あえてツッコミをいれると
1~5までの乱数を100個生成する。1~5までの数字の個数をその都度記録する
これを5回繰り返す。エクセルでINT(RAND()*5+1)をcountifで数えれば・・・
実行結果(26,18,21,21,14)(15,22,22,18,23)(17,25,25,17,16)(15,25,23,21,16)(24,16,18,23,19)
回数を多くすると11~35ぐらいまでは出てくることがありました。
またこの推論は6年前~2年前で検証し、1年前のデータで確認するみたいな感じでやるのが妥当と思われます。実質は1年前~5年前でデータ集計しているのでこれを6年前のデータで確認しても同様の試行ができると考えられる。
って感じですね。
>hiroさん
何度か読み返してやっと理解しました笑
そういうアプローチもなるほどなと思いつつ、結局は統計学未満の数遊びの域を出ないので、受験者がこういったことを真面目に考えるなら公式の確認に時間を使った方が生産的かと思います。
hiroさんや私みたいな電験が終わった人の贅沢な時間の使い方かなと笑
(しょーもないと言っているのでお分かりなんでしょうが)