皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
機械の電気機器以外の単元はマニアックなものが多いです。照明であったり、電気化学であったり、電熱であったり、、、出題される問題はそれぞれの単元の基本レベルに留まっているものの、門外漢が1から学んだ場合は難しい!の一言に尽きます。
私は幸い高校化学のバックグラウンドがありましたので、電気化学では電験で新たに勉強した箇所は少なかったです。というか、例のごとく単純暗記をして試験に備えていたのではなく、反応式の導出だけを抑えていました。実は、それだけで水の電気分解で発生する\(\mathrm{H}_2\)の体積を求める事ができます。
ということで、今回は化学の、とりわけ酸化還元反応について書いていきます。
到達イメージ

今回の紹介する導出ができるようになると、
水の電気分解では\(\mathrm{O}_2\)が陽極・陰極のどちらで発生するか
ということから、
水の電気分解で電流を流した時に、発生する\(\mathrm{H}_2\)の体積はいくらか
ということまで分かるようになります。
加えて、水の電気分解の反応式を書けるようになると、鉛電池の充放電式も書けるようになりますので、電気化学単元の勉強の省エネが進むはずです。
酸化還元反応とは

酸化還元反応とイオン反応の違いから話すと細かくなりすぎますので、そこを飛ばして更に水の電気分解に限定して説明していきます。
先ず、水\(\mathrm{H_2 O}\)中の\(\mathrm{H}\)と\(\mathrm{O}\)は、それぞれ酸化と還元の状態にあります。\(\mathrm{H}\)は\(\mathrm{H^+}\)、\(\mathrm{O}\)は\(\mathrm{O^{2-}}\)の状態にあると見なします。これは見方を変えると、
- \(\mathrm{H^+}\)は電子\(\mathrm{e}^-\)を1個失った状態
- \(\mathrm{O^{2-}}\)は電子\(\mathrm{e}^-\)を2個得た状態
と言えます。このように電子を失った状態を酸化と言い、電子を得た状態を還元と言います。
酸化と還元の状態は酸化数という概念でも表現することがあり、\(\mathrm{H_2 O}\)の\(\mathrm{H}\)は酸化数が+1、\(\mathrm{O}\)は酸化数が-2となります。
つまり、酸化還元反応とは反応の前後で酸化と還元の状態の遷移がある反応のことを言います。
タイトルにある「半反応式」とは
水の電気分解をした時は、水が水素と酸素に分かれます。これを個別に式に表すと
\(\mathrm{2H_2O} + \mathrm{2e^-} \to \mathrm{H_2} + \mathrm{2OH^-}\) …式1
\(\mathrm{2H_2O} \to \mathrm{O_2} + \mathrm{4H^+} +\mathrm{4e^-}\) …式2
となります。この\(\mathrm{e^-}\)が登場してくる水素と酸素で分けた個別の式を半反応式と言います。この半反応式の書き方には一定のルールがあり、これが書けるようになると鉛電池も含めて一気に電気化学の単元が楽になります。式1、2を例に立て方を説明していきます。
式1について
先ず、水が水素になるということを式で表します。
\(\mathrm{H_2 O} \to \mathrm{H_2}\) …式1-1
これだと、左辺に登場してくる\(O\)が反応後では消滅していることになってしまいます。これはおかしいので、右辺に何らかの形で\(O\)を存在させなければなりません。
ただ、\(\mathrm{O}\)は\(\mathrm{O^{2-}}\)で存在はしなく、水中では水酸化物イオン\(\mathrm{OH^-}\)という安定的なイオンの形で存在しています。式1-1では\(\mathrm{H}\)の数が等しいので、左辺に\(\mathrm{H_2 O}\)を1個だけ加えて\(\mathrm{O}\)を増やします。
\(\mathrm{2H_2O} \to \mathrm{H_2} + \mathrm{2OH^-}\) …式1-2
段々、形が式1に近づいてきました。あとは両辺のイオンのプラスマイナスを\(\mathrm{e^-}\)で調整するだけです。右辺の陰イオンが2個あるので、左辺に\(\mathrm{e^-}\)を2個加えて完了です。
\(\mathrm{2H_2O} + \mathrm{2e^-} \to \mathrm{H_2} + \mathrm{2OH^-}\) …式1
式2について
式1と似たような流れです。
水が酸素になるという式から出発します。
\(\mathrm{H_2O} \to \mathrm{O_2}\)
これだと\(\mathrm{O}\)の数が両辺で一致しないので、\(\mathrm{H_2O}\)で調整します。
\(\mathrm{2H_2O} \to \mathrm{O_2}\)
右辺に余る\(\mathrm{H}\)は、水素イオン\(\mathrm{H^+}\)という安定的なイオンとして存在します。
\(\mathrm{2H_2O} \to \mathrm{O_2} + \mathrm{4H^+}\)
最後は\(\mathrm{e^-}\)で調整して、
\(\mathrm{2H_2O} \to \mathrm{O_2} + \mathrm{4H^+} +\mathrm{4e^-}\)
となります。
半反応式が示していること

\(\mathrm{2H_2O + 2e^- \to H_2 + 2OH^-}\) …式1
\(\mathrm{2H_2O \to O_2 + 4H^+ +4e^-}\) …式2
式1,2をじっくりみてみましょう。式1では、水に電子を注入することで水素を作っています。式2では、逆に水から電子を奪いながら酸素を作っています。
ここで半反応式の理解を深めるために、水の電気分解を電気回路図チックに書いてみましょう。
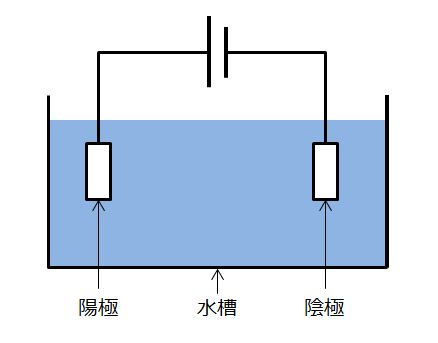
私が何を言いたいか何となく分かってきたでしょうか?この似非電気回路図をこんな風に書いたらどうでしょうか?
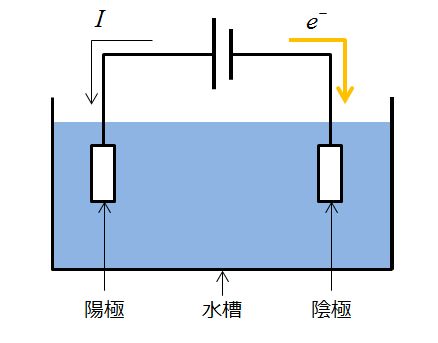
そうです。半反応式が書けると、↓のような図を何もないところから書けるようになります。
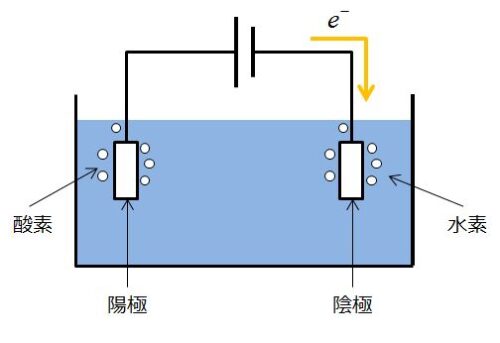
これが書けると、陽極(もしくは陰極)で発生する気体名を答えることができます。
半反応式から酸化還元式へ

エネルギー管理士や電験2種になると、発生した気体の体積を答えさせる問題が出ます。これも半反応式を書けていると解けます。
\(\mathrm{2H_2O + 2e^- \to H_2 + 2OH^-}\) …式1
\(\mathrm{2H_2O \to O_2 + 4H^+ +4e^-}\) …式2
2つの半反応式から1つの酸化還元反応式を作るには、\(\mathrm{e^-}\)をキャンセルするように2式を足します。つまり、式1×2+式2を計算します。
\(\mathrm{6H_2O \to 2H_2 + O_2 + 4H^+ +4OH^-}\) …式3
副生成物の\(\mathrm{H^+}\)イオンと\(\mathrm{OH^-}\)イオンは中和して、
\(\mathrm{H^+ + OH^- \to H_2O}\)
となるので、式3は
\begin{align}
\mathrm{6H_2O \to 2H_2 + O_2 + 4H_2O}\\
\mathrm{2H_2O \to 2H_2 + O_2}\\
\end{align}
となります。この反応には4個の電子が参加するので、
\(\mathrm{2H_2O \underrightarrow{ 4e^- } 2H_2 + O_2}\)
とも書きます。
例題
Q.\(100\mathrm{A}\) の電流を193秒間流して水を電気分解した際に発生する、標準条件下の水素の体積\((L)\)は?
A.流れる\(\mathrm{e^-}\)のモル数は\begin{align}100\mathrm{A} \times 193\mathrm{s} \times \frac{1}{96500\mathrm{C/mol}} = 0.20\mathrm{mol}\\ \end{align}となります。よって、発生する水素の体積は\begin{align}0.20\mathrm{mol} \times \frac{2}{4} \times 22.4\mathrm{L/mol} = 2.24\mathrm{L}\\ \end{align}となります。
まとめ
今回はかなり化学チックな内容となってしまいました笑
半反応式の導出方法を知っていると、かなり省エネでこの単元を消化できることがわかったかと思います。ただ、今回の内容は高校化学の中盤くらいでやる内容ですので、半反応式を理解するための説明にあった化学的な考え方の土壌が無いと、逆にこの方法はとても非効率なものになります。ご自身のバックグラウンドに合わせて単純暗記の方法と比較してみて下さい。
なお、鉛電池の充放電式も
\(\mathrm{Pb + PbO_2 + 2H_2SO_4 \underrightarrow{ 2e^- } 2PbSO_4 + 2H_2O}\)
半反応式で書けます。それは↓のおまけで書いていきます。
それでは次回!
おまけ
鉛電池の充電は放電の逆反応ですので、放電のみを説明していきます。
鉛電池の半反応式は以下の2つです。
\(\mathrm{Pb \to Pb^{2+} + 2e^-}\) …式3
\(\mathrm{PbO_2 + 4H^+ +2e^- \to Pb^{2+} + 2H_2O}\) …式4
式3について
鉛\(\mathrm{Pb}\)が陽イオン\(Pb^{2+}\)になるのを2個の\(e^-\)で調整しています。
式4について
基本の反応は
\(\mathrm{PbO_2 \to Pb^{2+}}\)
です。水の電気分解と同じように変形していくと、
\(\mathrm{PbO_2 + 2H_2O \to Pb^{2+} + 4OH^-}\)
となりますが、この反応は硫酸酸性中で起こっているので、水酸化物イオン\(\mathrm{OH^-}\)はすぐに硫酸の\(\mathrm{H^+}\)で中和されてしまいます。つまり、
\(\mathrm{PbO_2 + 2H_2O + 4H^+ \to Pb^{2+} + 4H^+ + 4OH^-}\)
\(\mathrm{PbO_2 + 4H^+ \to Pb^{2+} + 2H_2O}\)
となります。あとは\(\mathrm{e^-}\)で左右のイオン価数を調整して
\(\mathrm{PbO_2 + 4H^+ +2e^- \to Pb^{2+} + 2H_2O}\)
となります。
半反応式から酸化還元式へ
式3+式4から
\(\mathrm{Pb + PbO_2 + 4H^+ \underrightarrow{ 2e^- } 2Pb^{2+} + 2H_2O}\)
となります。\(\mathrm{H^+}\)は硫酸\(\mathrm{H_2SO_4}\)から供給されていますので、\(\mathrm{4H^+}\)分の発生源として硫酸イオン\(\mathrm{SO_4^{2-}}\)を2個両辺に加えます。
よって、
\(\mathrm{Pb + PbO_2 + 4H^+ + 2SO_4^{2-} \underrightarrow{ 2e^- } 2Pb^{2+} + 2SO_4^{2-} + 2H_2O}\)
\(\mathrm{Pb + PbO_2 + 2H_2SO_4 \underrightarrow{ 2e^- } 2PbSO_4 + 2H_2O}\)
となります。