皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
電験3種の勉強を初めて直ぐに、理論科目の電磁気学のところで公式の多さに辟易する方は多いと思います。
しかしできるだけ原則から覚えておけば、公式の対応を省エネできます。
今回は電磁気学の公式の中でも、似たような形で区別しにくい電流による磁界の公式を覚える方法をご紹介します。
「直線電流の周辺磁界」と「円形コイルの中心磁界」
電流が作る磁界の公式には、似て非なる2つの公式があります。それは「直線電流の周辺磁界」と「円形コイルの中心磁界」です。
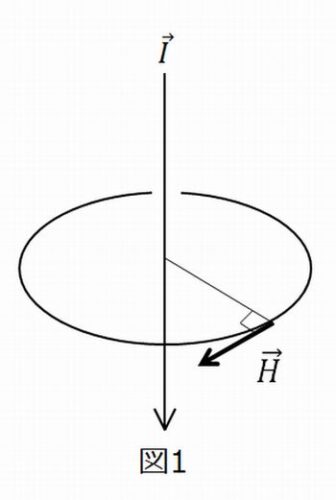
図1のような直流電流\(I\)による周辺磁界\(H\)を求める公式は
\begin{align}H=\frac{I}{2\pi r} …(1) \ \end{align}
となります。
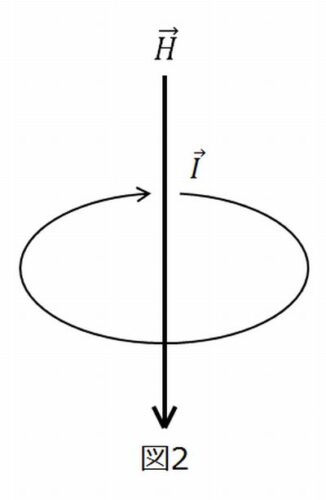
一方で、図2のような円形電流\(I\)による中心磁界\(H\)を求める公式は
\begin{align}H=\frac{I}{2 r} …(2) \ \end{align}
となります。
2つ公式を区別して覚えようとしたときに、イメージ図を頼りに覚えようとしても、図が似通っている上に公式は\(\boldsymbol{\pi}\)の有無しか違いがないので、苦労するのではないでしょうか。
こういった公式の背景にはそれぞれ別の汎用的な公式があって、その特殊な条件が公式(1)なり公式(2)になりに落ち着くというのが、電験の“あるある”です。この公式を押さえてしまおうというのが今回の趣旨です。
背景にある公式とは

公式(1)を導出するにはアンペアの周回積分の法則を使用して、公式(2)を導出するにはビオ・サバールの法則を使用します。
ただし、電験3種では公式名を答えさせる問題は出ません。回りくどい言い方をしているのは、電験2種では公式名を答えさせる問題が出るからです笑
電験2種までになるとどちらの法則もきちんと理解しておく必要がありますが、電験3種では簡単な方だけを押さえれば十分です。簡単な方の公式で導出した結果、その式に\(\pi\)があればもう片方の式は無い方を、\(\pi\)が無ければ片方はある方を、というふうにできます。
アンペアの周回積分の法則
アンペアの周回積分の法則の方が比較的簡単に公式を導出できます。アンペアの周回積分の法則のイメージは以下のようになります。
\(N\)本の導体にそれぞれ等しく電流\(I\)が流れているとき、ある閉じられた経路\(l\)に沿って磁界\(H\)を積分してくと、その値が\(NI\)に等しくなります。(図3)
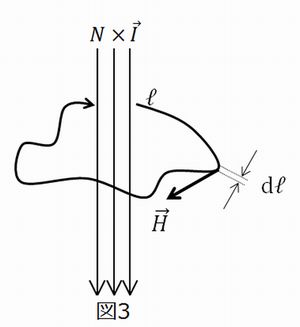
これを式に表すと
\begin{align}\displaystyle \int H\mathrm{d}l =NI …(3)\ \end{align}
となります。
もちろん、図4のような導線を中心に半径\(r\)の円でも問題ありません。
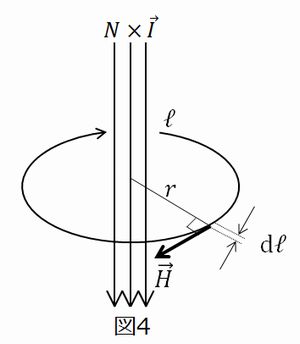
この場合、常に導体と磁界の距離が一定となるので公式(3)の左辺の\(H\)は定数となり、\(\int\) の外に出せます。
\begin{align}H\displaystyle \int \mathrm{d}l =NI …(3)\ \end{align}
更に、1周の長さは\(2\pi r\)なので、微小区間\(\mathrm{d}l\)を積み上げていった\(\int \mathrm{d}l\)は\(2\pi r\)となります。つまり、
\begin{align}H \times 2\pi r&=NI\\
H&=\frac{NI}{2\pi r} …(3)’\\ \end{align}
となります。
図4において\(N=1\)としたときが図1なので、式(3)’に\(\boldsymbol{N=1}\)を代入して公式(1)が得られます。
まとめ
電流による磁界の公式を思い出すときは、図4と公式(3)を覚えておくようにしましょう。そこから公式(1)を導出できれば、\(\boldsymbol{\pi}\)が無い方の公式も芋づる式に導出することができます。
理論科目以降の覚えることを考えると、公式の単純暗記は建設的ではありません。今回のように公式を覚えるのが大変だと感じたときは、その公式の背景にあるもう1つの公式を調べてみると意外と簡単に覚えられるかもしれません。
それでは次回!
おまけ
今回のメインのお話はアンペアの周回積分の法則からの導出でしたが、念のためにビオ・サバールの公式から公式(2)を導出する方法もご紹介しておきます。
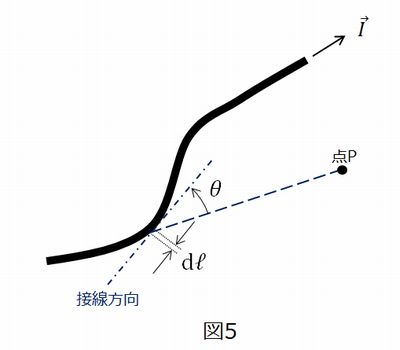
図5のようなぐねぐねと曲がった導体に電流\(I\)が流れているとき、微小区間\(\mathrm{d}l\)の導体が点P(距離\(r\))に発生させる磁界\(\mathrm{d}H\)は
\begin{align}\mathrm{d}H=\frac{I\mathrm{d}l\sin \theta}{4\pi r^2}\ \end{align}
となります。
これを図2に変形していきます。

先ず、両辺を積分して
\begin{align}\displaystyle \int \mathrm{d}H&=\displaystyle \int \frac{I\mathrm{d}l\sin \theta}{4\pi r^2} …(4)\
\end{align}
となります。
導体の接線方向と円の中心方向のなす角は常に90°で、半径\(r\)も常に一定です。また、1周の長さは\(2\pi r\)なので、微小区間\(\mathrm{d}l\)を積み上げていった\(\int \mathrm{d}l\)は\(2\pi r\)となります。
したがって式(4)は、
\begin{align}H&=\displaystyle \int \frac{I\mathrm{d}l\sin 90^{ \circ }}{4\pi r^2}\\
&=\frac{I}{4\pi r^2}\displaystyle \int \mathrm{d}l\\
&=\frac{I}{4\pi r^2}\times 2\pi r\\
&=\frac{I}{2r}\\
\end{align}
となります。














