皆さまお疲れさまです。ケンタ(@den1_tanaoroshi)です。
電験の各単元を理解していく上で原理を抑えておくと、数値関係の暗記は省エネすることができます。これは当ブログの至る所で言ってきたことです。
今回は、電験3種過去問再挑戦の理論編で書いていた「風力発電の出力は風速の3乗に比例する」というところを書いていきます。
「エネルギー」と言えば

運動エネルギー\(\boldsymbol{\frac{1}{2}mv^2}\)です。
この運動エネルギー自体の導出は運動方程式をエネルギー積分することでできますが、微分方程式とか合成関数の微分とかの知識が必要ですので、いっそのことこれについては覚えてしまったほうが楽です。
今回は\(\frac{1}{2}mv^2\)に「風が吹いている状態」を代入していきます。
風が吹いている状態を当てはめる
先ず、運動エネルギー\(\frac{1}{2}mv^2\)が、どのような対象のどのような物理量を示してるかを改めて考えてみましょう。
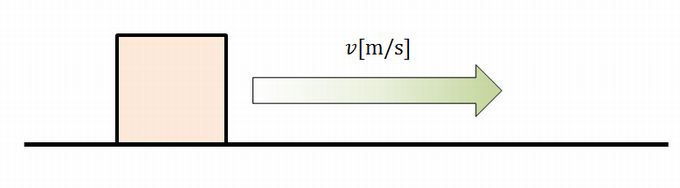
質量が\(m[\mathrm{kg}]\)の物体(今回は仮に立方体とします)が速度\(v[\mathrm{m/s}]\)で運動している時の、物体の持つエネルギーを運動エネルギー\(\frac{1}{2}mv^2\)としています。
これを「風」で例えてみます。
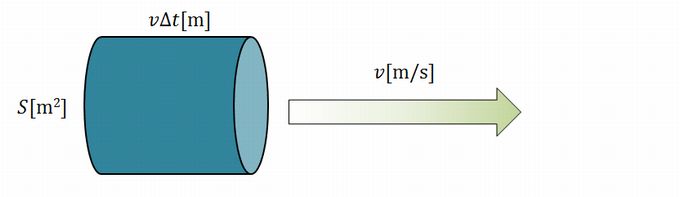
風の質量については、ある断面\(S[\mathrm{m^2}]\)と風速\(v[\mathrm{m/s}]\)と風が吹く時間\(\varDelta t[\mathrm{s}]\)を使って、風の体積を\(Sv\varDelta t[\mathrm{m^3}]\)と設定します。空気の密度が\(\rho[\mathrm{kg/m^3}]\)であった時、その体積の質量は\(\rho Sv\varDelta t[\mathrm{kg}]\)となります。
この質量の風が風速\(v[\mathrm{m/s}]\)で移動しているので、その運動エネルギー(E\)は
\begin{align}
E&=\frac{1}{2}mv^2\\
&=\frac{1}{2}\rho Sv\varDelta t\times v^2\\
&=\frac{1}{2}\rho S\varDelta tv^3\\
\end{align}
となります。
次に、出力\(P\)は単位時間あたりのエネルギー\(E\)ですので、
\begin{align}
P&=\frac{E}{\varDelta t}\\
&=\frac{1}{2}\rho Sv^3\\
&\propto v^3\\
\end{align}
つまり、速度の3乗に比例することになります。
まとめ
過去問再挑戦でも書いていましたが、今回のような風力発電に関する「3乗」という知識は、運動エネルギーの公式だけ覚えていれば解答用紙の余白を使用して1から導出することができます。
この他にもまだまだ、導出のきっかけを覚えるだけで対処している独自知識がありますので、どんどん紹介していければと思います。
それでは次回!